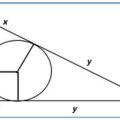
Decía J. Kepler (1571-1630): La Geometría tiene dos grandes tesoros: uno es el Teorema de Pitágoras, y el otro el Número Áureo. El primero puede compararse a una medida de oro, y el segundo a una piedra preciosa.
El Teorema de Pitágoras es, seguramente, el teorema más famoso de la Geometría. En él están contenidas las ideas fundamentales de perpendicularidad y de distancia entre dos puntos del espacio en el que nos movemos.
El Teorema de Pitágoras dice que en todo triángulo rectángulo, si b y c son las medidas de los catetos (lados que forman el ángulo recto) y a es la hipotenusa, se cumple que a² = b² + c².
Es posible que esta relación general para cualquier triángulo rectángulo fuera descubierta en la Escuela Pitagórica, pero, cuenta Herodoto (484- 425 a. C.) que en el antiguo Egipto, los agrimensores conocían esta relación, al menos para un triángulo rectángulo particular, y la utilizaban para rehacer cada año los límites de las parcelas de los agricultores que quedaban borradas por las inundaciones producidas por los desbordamientos del Nilo y que entre los utensilios técnicos que usaban estaba una cuerda dividida mediante nudos en doce espacios de igual longitud. Con la que podían formar un ángulo recto.
Esta labor la realizaban entre tres trabajadores (llamados por Herodoto tensadores de cuerda) un trabajador mantenía unidos los dos extremos de la cuerda, otro sujetaba el nudo que distaba tres espacios a partir de uno de los extremos, y el tercer tensador sujetaba el nudo que situado a cuatro espacios del otro extremo de la cuerda. Cuando tensaban la cuerda, se formaba un ángulo recto y un triángulo rectángulo de lados 3, 4 y 5 tal como se observa en la figura, que cumple la relación 5² = 4² + 3².
Se llaman Ternas Pitagóricas a las ternas (a, b, c) de números enteros positivos que satisfacen el Teorema de Pitágoras o, equivalentemente, que tríos de números enteros que son los lados de un triángulo.
Se puede pensar que las Ternas Pitagóricas son escasas o difíciles de encontrar. Los agrimensores egipcios encontraron que un triángulo de lados tres cuatro y cinco era rectángulo, pero también sabían que si elegimos arbitrariamente la longitud entera de los catetos, la hipotenusa no será, en general, un número entero.
No obstante, conocida una Terna Pitagórica (3, 4, 5) podían obtenerse infinitas Ternas proporcionales, como (6, 8,10), (9, 12, 15 ), ( 12, 16,20), … , (3n, 4n, 5n)…
HAY INFINITAS TERNAS PITAGÓRICAS NO SEMEJANTES
La demostración la basaremos en dos ideas gdfundamentales:
Primera: La diferencia de los cuadrados de dos enteros consecutivos es un número impar y recíprocamente, todo impar es diferencia de dos cuadrados de números consecutivos.
En efecto: (n + 1)2 – n2 = (n2 + 2n + 1) – n2 = 2n + 1
Segunda: Como el cuadrado de un número impar es impar, hay infinitos números cuadrados que son impares. De hecho, hay infinitos cuadrados impares, ya que a cada número impar le corresponde un cuadrado impar, ya que :
Si a es impar, se puede expresar en la forma a = 2n+1, con n entero a le corresponde univocamente uncuadrado impar a2 , y que
a2 = (2n + 1)2 = 4n2 + 4n + 1 = 4(n2 + n) + 1 = 4k +1, por lo tanto es impar.
Por otra parte, como a cada a le corresponde uno y sólo un cuadrado y cada impar cuadrado se puede expresar como diferencia de dos cuadrados. Euclides y los geómetras griegos lo razonarían geométricamente, observando la figura dormada por un cuadrado de lado n+1
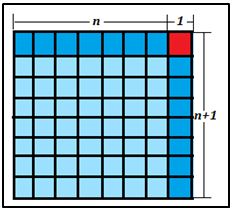
imponiendo que el gnomon 2n + 1 = a2 ⇒ n = (a2 – 1)/2.
Como a2 es impar entonces a debe ser impar. Las infinitas ternas serán (a, n y n+1), que cumplen que a2 +n2 = (n+1)2 se obendrán dándole a a valores impares y teniendo en cuenta que n = (a2 – 1)/2 y podemos escribir:
(3, 4 y 5); (5, 12 y 13); (7, 24 y 25); (9, 40 y 41);
(11, 60, 61); (13, 84 y 85); (15, 112, 113)…
De este modo, se obtienen las infinitas Ternas Pitagóricas en las que la diferencia entre la hipotenusa y uno de los catetos es una unidad.
OTRAS FORMAS DE OBTENER TERNAS PITAGÓRICAS
Hay otras formas de obtener Ternas Pitagóricas, a partir de la fórmula del cuadrado de una suma:
Primera: Teniendo en cuenta que (a+1)2 = (a-1)2 + 4a, haciendo a = n2
Se obtiene que (n2+1)2 = (n2-1)2 + (2 n)2 y, a partir de esta relación:
Ternas del tipo (2n, n2 -1, n2 +1) n ≥ 2, de donde se obtienen:
(4, 3, 5); (6 8,10); (8, 15, 17); (10, 24, 26); (12, 35 37); …
Segunda: Análogamente de la identidad: (a + b)2 = (a – b)2 + 4 ab
Haciendo a = m2 y b = n2 se obtiene la expresión:
(m2 + n2)2 = (m2 – n2)2 + 4 m2 · n2 ⇒ se cumple que
(m2 + n2)2 = (m2 – n2)2 + (2n·m)2
Y Ternas del tipo (2mn, m2 – n2, m2 + n2) con m > n >0.
Tercera: La sucesión de Fibonacci tiene una estrecha relación con las Ternas Pitagóricas. La sucesión se forma por la ley de decurrencia:
Fn+2 = F n+1 + F n con F1 = 1 y F2 =1
es decir, la sucesión:
1 , 1, 2, 3, 5 , 8, 13, 21, 34, 55, 89, 144, 233 ….
Tomando cuatro elementos consecutivos de la sucesión: Fn , F n+1, F n+2 y· F n+3
1- Sea A el producto de los números que ocupan los extremos A = Fn· F n+3.
2- Sea B el doble del producto de los números intermedio B = 2 F n+1· F n+2.
3- Sea C es la suma de los producto de los números que están en posición impar más producto de los números que están en posición par. C = Fn·F n+2, + F n+1· F n+3
Tomando, por ejemplo, los cuatro elementos de la sucesión : 3, 5 , 8, 13, se tiene:
A = 3·13 = 39 ⇒ A2 = 392 = 1521
B = 2·5·8 = 80 ⇒ B2=802 = 6400
C = 3·8 +5·13 = 24 + 65 = 89 ⇒ C2 = 892 = 7921
La Terna (A, B, C) = (39, 80, 89) cumple que C2 = A2 + B2
Se cumple en general: Si para facilitar los cálculos hacemos:
Fn = a, F n+1 = b, F n+2 = a+b, F n+3 = a+2b
Entonces (a, b, c) es una terna pitagórica, ya que .
A = a(a +2b) ⇒ C 2= a4 + 4a2b2+ 4 a3 b
B = 2 b(a + b) ⇒ B2 = 4a2b2+ 4b4 + 8 a b3
C = a(a + b) +b (a+2b) ⇒ C 2 = a4 + 4·a3 ·b + 8·a2 ·b2 + 8·a·b3 + 4·b4
Puede comprobarse que C2 = A2 + B2