
Galileo Galilei (1564-1642) describió la noción de Sistema de Referencia Inercial con un experimento mental que definió en su obra Diálogos sobre los dos máximos Sistemas del Mundo: el Tolemaico y el Copernicano (1632) con estas palabras:
Enciérrate con un amigo bajo cubierta en la cabina principal de un barco grande, y lleva contigo algunas moscas, mariposas y otros animalillos voladores. Lleva también un recipiente grande de agua con unos peces; cuelga una botella que se vacíe gota a gota en un recipiente ancho colocado debajo. Cando la nave está en reposo, observa cómo los insectos vuelan con la misma velocidad en cualquier parte de la cabina. Los peces nadan indiferentemente en todas direcciones; las gotas de la botella de agua caen en el recipiente que está debajo; y, al lanzar algo a tu amigo, no necesitarás tirarlo con mayor fuerza en una dirección que en otra, si las distancias son iguales; al saltar con los pies juntos, avanzarás la misma distancia en cualquier dirección. Cuando hayas observado todos estos hechos con cuidado (cuando la nave está parada), haz que la nave avance con la velocidad que desees, siempre que el movimiento sea uniforme y no fluctúe de una u otra manera (sea rectilíneo). Descubrirás que no hay el menor cambio en todos los efectos nombrados, ni podrás decir, a partir de ninguno de ellos, si se estás en un barco en movimiento o en un barco en reposo.
Con esta descripción Galileo ponía de manifiesto que no era posible distinguir entre los sucesos que se producían en un Sistema de Referencia en reposo y los que sucedían en cualquier otro Sistema de Referencia que se desplazaba con un movimiento rectilíneo y uniforme respecto a él.
Un sistema de referencia inercial no se distingue de un sistema en reposo porque no está sometido a fuerzas exteriores y no hay, por tanto, aceleraciones, ni cambios de velocidad y en ellos se conserva el momento lineal: p = mv. Cuando un sistema de partículas no recibe impulso del exterior, su momento lineal total es constante.
Galileo estableció unas leyes de transformación para relacionar las ecuaciones de movimiento calculadas desde dos sistemas de referencia inerciales distintos. Estas transformaciones formaron parte de la base de la Mecánica Newtoniana.
Tomemos dos sistemas inerciales, S y S’. Un punto P que tiene de coordenadas (x,y,z) en el sistema de referencia inercial S, y (x’,y’,z’) en el sistema de referencia inercial S’ que se mueve con una velocidad constante, v, en sentido positivo a lo largo del eje X del sistema S.
Hemos de recordar que en la mecánica Newtoniana-Galileana el tiempo era absoluto para cualquier observador con independencia del sistema de referencia inercial en que se encontrara, ( t = t´). En palabras de Newton:
El tiempo absoluto, verdadero y matemático, en sí y por su propia naturaleza sin relación a nada externo fluye uniformemente, y por otro nombre se conoce como duración. El tiempo relativo, aparente y vulgar es una medida sensible y exterior, precisa o imprecisa, de la duración mediante el movimiento, usada por el vulgo en lugar del verdadero tiempo; hora, día, mes y año, etc.
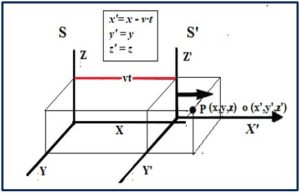
Con estos supuestos podemos entender que las transformaciones de Galileo toman la siguiente forma:
x’ = x – vt (x = x’ + vt), y’= y, z’= z, t = t’
La relación entre las velocidades de P en los sistemas S y S’ están se pueden obtener a partir de las relaciones anteriores derivando respecto al tiempo (como el desplazamiento se realiza a lo largo del eje OX):
dx’/dt = dx/dt + v o, expresado de otro modo: vs’ = vs – v
Lo que significa que si un punto se mueve en el sistema S a una velocidad vs, en el sistema S’ (que se desplaza a una velocidad v respecto a S) se moverá a una velocidad vs’, que será la suma algebraica de v con vs.
Este resultado de las transformaciones de Galileo tiene una importancia capital.
En primer lugar, como vs’ = vs – v, se cumple que en dos sistemas de referencia inerciales que se muevan con velocidad relativa v ≠ o, las velocidades de un objeto medidas desde S y S’ tienen que ser distintas (vs’ = vs – v y v ≠ o ⇒ vs’ ≠ vs) por lo tanto, no puede existir un objeto que tenga la misma velocidad en cualquier sistema de referencia inercial.
En los sistemas no inerciales hay variación del momento lineal:
![]()
En estos sistemas se cumplen, por extensión los otros dos principios de la dinámica de Newton.
Galileo enunció que, desde cualquier sistema de referencia inercial se observan las mismas leyes físicas (lo que significa que desde todos ellos se miden las mismas fuerzas). Además, si v es constante a lo largo de su dirección paralela al eje X (por tanto, en línea recta). Las leyes de la mecánica newtoniana tendrán la misma expresión, puesto que las aceleraciones serán las mismas en ambos sistemas (F=m·a invariable)
dx/dt = dx’/dt + v ⇒ d2x/dt2 = d2x’/dt2 = a
Estas transformaciones entre sistemas inerciales hacen que las leyes de la mecánica sean las mismas para todos ellos. Dos sistemas de referencia con movimiento de traslación rectilínea y uniforme son equivalentes desde el punto de vista mecánico; es decir, los experimentos mecánicos que se desarrollan en uno se realizan de igual forma en el otro, y las leyes de la mecánica son las mismas.
Pero el electromagnetismo iba a perturbar la ley de la suma de velocidades que acabamos de mostrar. En este campo surgió por primera vez una velocidad en el mundo físico que no seguía las leyes de Galileo referentes a la suma de velocidades. La velocidad de un proyectil dependía de la velocidad que con que la lanzaba el cañón pero incrementaba o disminuía la velocidad la velocidad que llevaba del cañón que lo lanzaba. Para justificar la anomalía de la velocidad de la luz haremos el siguiente resumen:
a) Cuando en 1746 J. D’Alembert (1717-1783) estudió la ecuación de una onda Ψ(x,t) obtuvo la siguiente expresión en forma de ecuación diferencial, en la que aparecía v, que era la velocidad de desplazamiento de la onda:
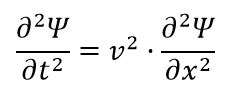
b) Por otra parte, en las leyes del electromagnetismo de J. C. Maxwell (1831.1879) en las que se condensaban los descubrimientos realizados por Faraday , Gauss , etc y describían perfectamente lo que se observaba en los experimentos.
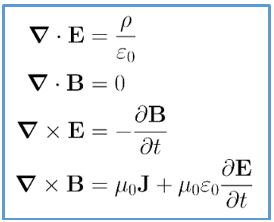
Las ecuaciones de Maxwell habían predicho la existencia de ondas electromagnéticas. En ellas aparecía la velocidad de la luz en el vacío, c, como constante, además, tanto el campo eléctrico como el magnético tenían la expresión de una onda electromagnética.
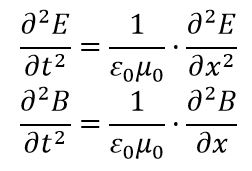
Velocidad de la onda electromagnética sería:
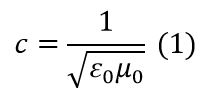
Lo que sugería que c sería constante con independencia del sistema inercial en el que se midiera su desplazamiento.
єo = 8,541878176×10-12 C2 / (N·m2) es la permitividad eléctrica del vacío y mide la capacidad de una sustancia para verse afectada por un campo eléctrico.
μ0 = 4Pi x 10-7 N·A-2 es la permeabilidad magnética o constante magnética, que es la capacidad de una substancia para atraer y permitir el paso de campos magnéticos a través de ella.
La permitividad eléctrica y la constante magnética del vacío están relacionadas por la fórmula (1).
Como c es la velocidad de la luz en el espacio vacío. Lo que indica es que c es constante con independencia del sistema inercial en el que se desplace. Pero la velocidad, en la Física Clásica, no era una magnitud absoluta independiente del sistema inercial en el que se encuentre como se consideraban la distancia, la superficie o el tiempo.
Las Leyes de Maxwell, que resumían el comportamiento de la electricidad y del magnetismo, en una nueva rama de la física que se denominó electromagnetismo habían llevado a la física una situación en la que había que decidir si las leyes de Maxwell eran incorrectas y, por tanto, había que rechazarlas o descubrir si existía un sistema inercial privilegiado por el que las ondas electromagnéticas se podían desplazar con velocidad constante, ya que las ondas de la física clásica no se propagaban en el vacío y necesitaban un medio material por el que propagarse.
Las transformaciones de Galileo no cubrían la mecánica y el electromagnetismo y pero eso lo harían las transformaciones de Lorentz-Einstein.


