
Hoy consideramos que las matemáticas y la física son dos materias que van de la mano en el estudio de naturaleza. Los cálculos, el método métodos y las estructuras matemáticas vertebran las teorías físicas. En el siglo XIX, el matemático alemán K. Weierstrass (1815-1897) destacaba la importancia de las matemáticas en las ciencias diciendo: No hay certidumbre allí donde no es posible aplicar ninguna de las ciencias matemáticas ni ninguna de las [otras ciencias]basadas en las matemáticas. Pero esto no siempre se ha entendido así. En la antigua Grecia se pensaba que la aproximación al conocimiento del mundo físico se podía realizar sin el concurso de las matemáticas y, más todavía, el propio Aristóteles (384-322 a.C.) llegó a afirmar que las matemáticas no contribuían al conocimiento de la esencia de las cosas y que, por consiguiente, poco podían contribuir a enriquecer su conocimiento.
Aristóteles criticó el papel que concedía la Escuela Pitagórica a los números. Los Pitagóricos pensaban, según Aristóteles, que todo lo que existía en el mundo, estaba formado según relaciones numéricas y que el número representaba las armonías y las analogías de todo lo que existe y jugaban el papel de los cuatro elementos de Empedocles: aire, fuego, la tierra y el agua. Aristóteles dice en el Libro Primero de su Metafísica, 980a-993a (De los Pitagóricos. Doctrina de los números. Parménides, Jenófanes, Meliso)
… los llamados Pitagóricos se dedicaron pronto a las matemáticas, e hicieron progresar esta ciencia. Embebidos en este estudio, creyeron que los principios de las matemáticas eran los principios de todos los seres. Los números son por su naturaleza anteriores a las cosas [son seres y no cosas abstractas], y los Pitagóricos creían percibir en los números más bien que en el fuego, la tierra y el agua, una multitud de analogías con lo que existe y lo que se produce. Tal combinación de números, por ejemplo, les parecía ser la justicia, tal otra el alma y la inteligencia, tal otra la oportunidad; y así, poco más o menos, hacían con todo lo demás; por último, veían en los números las combinaciones de la música y sus acordes. Pareciéndoles que estaban formadas todas las cosas a semejanza de los números, y siendo por otra parte los números anteriores a todas las cosas, creyeron que los elementos de los números son los elementos de todos los seres, y que el cielo en su conjunto es una armonía y un número. Todas las concordancias que podían descubrir en los números y en la música, junto con los fenómenos del cielo y sus partes y con el orden del Universo, las reunían, y de esta manera formaban un sistema. Y si faltaba algo, empleaban todos los recursos para que aquél presentara un conjunto completo. Por ejemplo, como la década parece ser un número perfecto, y que abraza todos los números, pretendieron que los cuerpos en movimiento en el cielo son diez en número. Pero no siendo visibles más que nueve, han imaginado un décimo, el Antichton
Precisamente consideramos que los pitagóricos fueron los primeros que aplicaron las Matemáticas al estudio de la Física. Pitágoras de Samos (582-507 a.C.) dio un enorme impulso a las matemáticas y fue el primer filósofo que observó comportamientos semejantes y ciertos paralelismos entre los números y los fenómenos naturales.
De la Escuela Pitagórica surgió el descubrimiento de que los sonidos armoniosos de las cuerdas de la lira guardaban relación con la longitud de las mismas. Pitágoras encontró una conexión entre las matemáticas y la música que permitía relacionar las notas musicales con los números racionales. Para realizar sus investigaciones musicales construyó el monocordio, que era un instrumento musical de una sola cuerda que constaba de una caja de resonancia, de un canon (o regla graduada) y de un puente variable, que permitía hacer sonar diferentes longitudes de cuerda. Con el monocordio se podían medir las relaciones numéricas entre diferentes longitudes de cuerda que emitían los sonidos consonantes.
Pitágoras se apoyaba en que los intervalos musicales que había entre las notas armónicas de la lira podían expresarse numéricamente. Pero, además, los pitagóricos concibieron los números con una representación geométrica (en triángulos, cuadrados, cubos o pirámides), y llegaron a identificar el punto geométrico con la unidad aritmética con lo cual, las unidades aritméticas tenían extensión espacial y podían ser consideradas como los elementos materiales que formaban las cosas. Aceptada esta idea, toda la materia existente se podía considerar como agregados de puntos materiales y, por tanto, como conjuntos de unidades numéricas.
Las investigaciones de Pitágoras en acústica le hicieron concebir la idea de que todo lo que existía en la Naturaleza, desde lo más concreto hasta lo más abstracto, estaba sometido a las leyes de los números. Con la Escuela Pitagórica comenzó el estudio de la música como ciencia cuantitativa y de la medida. El propio Pitágoras descubrió una serie de relaciones aritmético-musicales que constituyeron el inicio de la ciencia musical y, seguramente, el primer ejemplo histórico de experimentación científica.
El pitagórico Jámblico (245-325) relataba, seguramente distorsionada y contada ocho siglos después, una historia de leyenda, en la que detallaba el descubrimiento de Pitágoras de la siguiente forma: al pasar Pitágoras por una herrería, le atrajeron los sonidos que producían los martillazos de cuatro esclavos al golpear sobre el yunque un trozo de metal. Tres de ellos producían sonidos consonantes, mientras que el cuarto producía una disonancia con ellos.
Creyendo el sabio que el sonido dependía de la fuerza con que golpeaban el yunque cada uno de los herreros, les pidió que se intercambiaran los martillos entre si, pero el resultado fue que el mismo martillo seguía produciendo el mismo sonido disonante cualquiera que fuera el herrero que lo utilizara. Pitágoras concluyó que la sonoridad no dependía de la fuerza de los esclavos, sino de las características de cada martillo. Al llegar a su casa, contaba Jamblico, que Pitágoras realizó la primera experiencia de laboratorio que registra la historia, pesó los martillos, ató sus pesos a cuerdas de igual longitud hasta que emitieran las mismas notas que daban los martillos, entonces descubrió que los tres consonantes tenían pesos proporcionales a 6, 8 y 12. Agregó después un trozo de arcilla, para modificar el peso del martillo, que producía desarmonía, hasta obtener un sonido agradable, en consonancia con los otros tres martillos, una vez añadida la arcilla, obtuvo la siguiente relación entre los pesos:
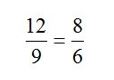
que, según Jámblico, se llama relación musical, porque contiene las relaciones musicales de los sonidos armónicos. De ahí salen las razones (1/2 (octava), 3/4(cuarta) y 2/3 (quinta)).
De esta forma, los Pitagóricos aceptaron como principio fundamental que los números eran el origen de todo y formaban parte la sustancia de las cosas, y concluyeron que cada objeto tenía un número o relación numérica que lo hacía diferente de los demás. Los pitagóricos pensaban que el número y las matemáticas formaban parte de la naturaleza de las cosas, del mismo modo que, a partir de Empédocles (494-430 a. C.), se aceptaron los cuatro elementos para formar la esencia de las cosas.
Víctor Arenzana Hernandez




