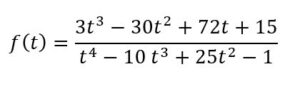
Lo que comúnmente se llaman problemas de resolución de ecuaciones algebraicas consiste en calcular los números que satisfacen esa relación. Los valores de la variable x que cumplen la ecuación x2 = 5x– 6 son 2 y 3 y son las soluciones de la ecuación.
En otros casos resolvemos otros problemas en los que la incógnita es una función como sucede en las ecuaciones diferenciales como f’(x) = 2f(x) que tiene por solución funciones del tipo f(x) = 2Ce2x.
Aquí analizaremos un tema relacionado sobre todo con el concepto de función. Se trata de encontrar todas o alguna de las funciones que cumplen una propiedad dada.
EJEMPLO 1: Determinar una función f (x) tal que f (x + 5) = x2 + 5x + 2.
La función f(x) será un polinomio de segundo grado.
Con el cambio de variable t = x + 5 ⇒ x = t – 5, f (x + 5) = x2 + 5x + 2 se transforma en f (t) = (t – 5)2 + 5(t – 5) + 2 = t2 – 5t + 2
⇒ f (t) = t2 – 5t + 2 que equivale a f (x) = x2 – 5x + 2 , por se x variable muda
EJEMPLO 2 : Determinar un polinomio P(x) que verifique que P(x2+1) = x4 + 6 x2
Lo determinaremos por dos procedimientos
Solución 1: Método de coeficientes indeterminados: Supongamos que P(x) = ax2 + bx + c
P(x2+1) = a (x2+1)2 + b (x2 + 1) + c = a x4 + (2 a +b ) x2 + a + b + c
Igualando coeficientes: a = 1, 2 a + b = 6, a + b + c = 0 ⇒ (resolviendo el sistema)
⇒ a = 1, b = 4 , c = -5 ⇒ P(x) = x2 + 4x -5
Solución 2: Cambio de variable t = x2 + 1= t ⇒ x2 = t -1
P(x2+1) = x4 + 6 x2 ⇒ P(t) = (t –1)2 + 6 (t – 1) = t2 + 4t -5 ⇔ P(x) = x2 + 4x -5
EJEMPLO 3: Encuentra f (x) si f (ln x) = x2 + x + 1, para x > 0.
Solución: Cambio de variable:
t = ln x ⇒ x = et f (t) = e2t + et + 1 ⇔ f (x) = e2x + ex +1
EJERCICIO 1.- Hallar una función f (x) que cumpla la siguiente ecuación f(1/(2x)) = x – 3f(x) (1)
Solución: Hacemos el cambio de variable t =1/(2x) ⇒ x = 1/(2t)
f(t) = 1/(2t) – 3f (1/(2t)), por la relación (1) f(1/(2t)) = t – 3 f(t) ⇒
⇒ f(t) = 1/(2t)) – 3[t – 3 f(t)] ⇒ f(t) = 1/(2t) – 3t + 9 f(t) ⇒
⇒ 8f(t) = 3t – (1/(2t)) ⇒ 8 f (t) = (6t2-1)/2t ⇒
⇒ f(t) = (6t2 -1 )/16t ⇔ f(x) = (6x2-1)/16x
EJERCICIO 2.- Hallar una función f (x) que cumpla la siguiente ecuación f(1/x) = x – 3f(x) (1)
Solución: Hacemos el cambio de variable t =1/x ⇒ x = 1/t
f(t) = 1/t – 3f (1/t)), pero,por la relación (1) f(1/t) = t – 3 f(t) ⇒
(sustituyendo) ⇒ f(t) = 1/t – 3(t – 3 f(t)) ⇒ f(t) = 1/t – 3t + 9 f(t) ⇒
⇒ 8f(t) = 3t – 1/t) ⇒ 8 f (t) = (3t2-1)/t ⇒
⇒ f(t) = (3t2 -1 )/8t ⇔ f(x) = (3x2-1)/8x
EJERCICIO 3.- Hallar una función f (x) que cumpla que 3f (2 – x) + 2 f (x) = x2 (2)
Solución:
t = 2 – x x = 2 – t la ecuación (2) se transforma en: 3 f(t) + 2f (2 – t) = (2 – t)2 (3)
y la podemos escribir con el cambio x = t como 3f (2 – t) + 2 f (t) = t2 (4)
Eliminando f (2 – t) entre las ecuaciones (3) y (4)
f(t) = (t2 -12t +12)/5 ⇔ f(x) = (x2 -12x+12)/5
EJERCICIO 4.- Hallar una función f (x) que cumpla que x2f(x) – f(5 – x) = 3x…(1)
Solución: Cambio de variable t = 5 – x ⇒ x = 5 – t la ecuación (1):
(5 – t)2 f (5 – t) – f(t) = 3(5 – t)
Recordamos que f(5 – t) está en la ecuación (1): t2f(t) – f(5-t) = 3t ⇒ f(5-t) = t2f(t) – 3t
(5-t)2 [t2 f(t) -3t)] – f(t) = 15-3t
[t2 (5 – t)2 -1]f(t) = 3t (5 – t)2 + 15-3t
(t4 – 10t3 + 25t2-1)f(t) = 3t3 – 30t2 + 75t + 15-3t
(t4 – 10t3 + 25t2 -1) f(t) = 3t3 – 30t2 + 72t + 15