
Las ecuaciones en diferencias tienen gran importancia en diferentes cuestiones y disciplinas que necesitan simular y modelizar la evolución de sistemas discretos. Se plantean en temas de como la ingeniería y la economía, dado que este tipo de modelaciones es más ajustado a la realidad. Las ecuaciones en diferencias abordan problemas en los que el objetivo determinar el valor de una función, f : Z → R para un n ∈ Z a partir de una o varias ecuaciones entre valores particulares de la función
Una ecuación en diferencias es una expresión del tipo:
F(n, f(n), f(n + 1), . . . , f(n + k)) = 0, ∀n ∈ Z,
donde f es una función definida. Si después de simplificar esta expresión quedan los términos f (n + k1) y f (n + k2) como el mayor y el menor, respectivamente, se dice que la ecuación es de orden k1– k2.
El caso más sencillo es el de la ecuación lineas:
a0f(n + k) + a1f(n + k − 1) + . . . + akf(n) = g(n), con ai ∈ R
La ecuación en diferencias se dice homogénea cuando g(n) = 0, y completa en el caso contrario. La más sencilla es la ecuación lineal homogénea de primer orden
ECUACIÓN EN DIFERENCIAS LINEAL HOMOGÉNEA Y DE PRIMER ORDEN CON COEFICIENTES CONSTANTES:
Ecuación lineal de primer orden: y(n) = a·y(n-1) ai ∈ R
Daremos a n sucesivamente los valores 1, 2, 3,…, n
y(1) = a·y(0)
y(2) = a·y(1) = a2 y(0)
y(3) = a·y(2) = a3 y(0)
….
y(n) = a·y(n-1) = an y(0)
y(0) = K
La solución de la ecuación en diferencias y(n) = a·y(n-1) ai ∈ R es
y(n) = K an o y(n) = an y(0)
Ejercicio: Cierta población de animales aumenta cada año un 15% ¿en cuántos años se duplicará?
Solución: Cada año la población se multiplica por el factor 1,15, la ecuación en diferencias que representa el proceso será: y(n) = 1,15 · y(n-1), [aquí a = 1,15] Si la población inicial en el año 0 es y(0), queremos saber dentro de cuantos años, n, la población y(n) será el doble de la inicial, es decir, cuando
y(n) = 2 y(0), como la solución de la ecuación es: y(n) = 1,15n y(0),
La población se duplicará cuando y(n) =2 y(0) , es decir, cuando
1,15n y(0) = 2 y(0) ⇒ 2 = 1,15n ⇒ 2 = 1,15n ⇒ n = log2/log 1,15 ⇒
⇒ n = 0,301030/0,060697 ≈ 5años
ECUACIÓN EN DIFERENCIAS LINEAL COMPLETA Y DE PRIMER ORDEN CON COEFICIENTES CONSTANTES:
Expresión general: y(x+1) = ay(x) + b
Obtendremos la formula de la solución dando a x sucesivamente los valores 1, 2, 3,…, n
x=1 y(1) = a·y(0) + b
x=2 y(2) = a·y(1) = a (a·y(0) + b) + b = a2 y(0) + ab + b
x=3 y(3) = a·y(2) = a (a2 y(0) + ab + b) + b = a3 y(0) + a2b + ab + b
…..….
x= n y(n) = an y(0) + b(an-1 + an-2 +…+ 1) ⇔ (recordando la suma de n términos de una progresión geométrica)
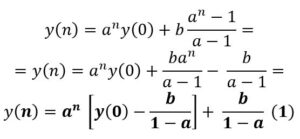
Ejemplo: Resolver y(n) = 2y(n-1) + 3 con el valor inicial y(0) =1
Solución: Aplicando la fórmula (1): como en esta ecuación a = 2 y b = 3
y(n) =2n (1-3/(-1)) -3 = 2n(4)-3 = 2n+2 – 3
Ejercicio: Cierta población se animales aumenta cada año un 20%. Si cada año se cazan 80 ejemplares y la población inicial es de 500. Escribe la ecuación en diferencias que describe la evolución de la especie.
Solución: La ecuación será y(n) = 1,20 · y(n-1) – 80 con el valor inicial y(0) = 500
Resolveremos la ecuación aplicando la fórmula general (1) con a = 1,20, b =-80
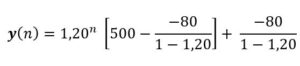
y(n) =100·1,20n +400
Crece indefinidamente.
Ejercicio: Cierta población se animales aumenta cada año un 15%. Si cada año se cazan 160 ejemplares y la población inicial es de 1000. Escribe la ecuación en diferencias que describe la evolución de la especie.
Solución: Se extinguirá el año n en que cuando y (n) = 0. La ecuación que describa la evolución de un año al siguiente será:
y(n) = 1,15 · y(n-1) – 200
…..
Crece indefinidamente.
Ejercicio: Cierta población se animales aumenta cada año un 15%. Si cada año se cazan 160 ejemplares y la población inicial es de 1000. Escribe la ecuación en diferencias que describe la evolución de la especie.
Solución: Se extinguirá el año n en que cuando y (n) = 0. La ecuación que describa la evolución de un año al siguiente será:
y(n) = 1,15 · y(n-1) – 200
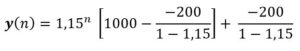
y(n) = 1,15n · (-333) + 1333
Se extinguirá el año n cuando y(n) = 0, es decir:
333· 1,15n · = (1067)
Log (333) + n log 1,15 = log 1067
n log 1,15 = log 1067 – log 333
n 0,061= 3.03 – 2,52
0,061n = 0,51 n = 8,36
Se extinguirá en 8 años y cuatro meses aprox.
