Se suele decir que Egipto fue la patria de la Geometría. Así lo creían varios pensadores griegos relevantes: el historiador Herodoto (484-425) decía que el origen de la Geometría estaba en la reparcelación que los agrimensores egipcios tenían que hacer de las tierras anegadas, después de las crecidas anuales del Nilo, con las lindes de las fincas cubiertas de limo. Por su parte, Aristóteles (385-323 a. C.) también le dio a Egipto esta prioridad, pero se inclinaba a pensar que los pioneros de los estudios geométricos estaban entre la clase sacerdotal ociosa egipcia, que habían lanzado sus especulaciones hacia cuestiones abstractas elevándose sobre el conocimiento práctico de la naturaleza.
Indudablemente, los puntos de vista del geógrafo y del filósofo eran diferentes, pero ambos presentaban dos caras de una misma moneda, Herodoto puso de manifiesto lo que podía contar un geógrafo que describía y analizaba lo que observaba y Aristóteles que se ponía el acento en la presentación de los conocimientos geométricos elaborados y estructurados racionalmente como los Elementos de Hipócrates de Chios (470-410 a. C.), de León, conocido como el geómetra, o de Teudio de Magnesia (c. IV a.C.).
De todos modos, el prestigio de la Geometría dentro del pensamiento griego era enorme; en la Academia de Platon (427-347 a. C.), fundada en 387 a.C, presidía el lema nadie entre aquí que no sepa geometría, lo que manifestaba la importancia que se le concedía a este saber en la institución platónica. En el Libro VI de Achitectura (27-23 a.C.), M. Vitruvio (81-15 a.C.) recogió una anécdota en este sentido y contaba que el discípulo de Sócrates, Aristipo de Cirene (435-350 a. C.) sufrió un naufragio en la costa de Rodas y, al percibir algunos diagramas geométricos se dirigió a sus compañeros para tranquilizarlos, y les dijo: aquí hay signos de civilización y se dirigieron hacia la ciudad.
La Geometría Griega, nadando inicialmente entre el saber práctico y el saber especulativo. realizó una gran aportación que fue la de transformar los descubrimientos empíricos de la geometría egipcia, en un saber teórico en el que las propiedades de las figuras y las diferentes relaciones entre las magnitudes se demostraban según un proceso lógico- deductivo a partir de una serie de principios fundamentales, llamados axiomas, postulados y definiciones siguiendo unas reglas lógicas firmemente establecidas. El proceso se inició con Tales de Mileto (624-546 a.C.) y Pitágoras de Samos (569-465 a. C.) y alcanzó su forma definitiva con los Elementos (300 a.C.) de Euclides (325-265), que se mantuvo como libro de texto más de dos mil años.
La Geometría griega fue uno de los logros más grandes del pensamiento de la antigüedad. Había logrado resolver problemas algunos prácticos: habían logrado trasformar unas figuras en otras de igual área, incluso cuadrar figuras de contorno curvilíneo. También se había planteado tareas particulares como la resolución de problemas con el uso de la regla y compás o el estudio de los poliedros regulares. Además, los geómetras se habían propuesto analizar si su propia forma de razonar era correcta y estaba libre de paradojas. La variedad de temas tratados y la necesidad de dar validez a sus resultados hicieron que fuera necesario consolidar el conocimiento geométrico y dotarlo de un orden estructurado con el método axiomático-deductivo, lo que hizo de la geometría un cuerpo de saber sólido, que se consideraba verdadero porque cada proposición se podía obtener de otra anterior, que era también verdadera, mediante un razonamiento lógico y retroceder sucesivamente hasta llegar a las primeras proposiciones aceptadas que se eran verdaderas por ser evidentes y se habían establecido como axiomas.
Pero la Ciencia Moderna convirtió a la Geometría Euclidiana en algo más: identificó a la Geometría con el espacio en el que vivimos. ¿Cuáles fueron las razones por las que el modelo euclidiano de Geometría fuera el modelo del espacio? ¿Por qué en veinte siglos de vida de la Geometría nadie había reparado que nuestro espacio era el espacio euclidiano?

Las razones hay que buscarlas, como precisamente destaca A. Koyré (1892-1964) en su libro Del mundo cerrado a universo infinito, en el cambio de visión que se produjo en siglo XVII, cuando la ciencia abandonó el modelo del mundo cerrado Ptolemaico-Aristotélico de las esferas cristalinas y adoptó el modelo de mundo en el espacio infinito, que culminaría espacio newtoniano propuesto por la Ciencia Moderna.
Debemos recordar que el mundo griego Ptolemaico-Aristotélico estaba configurado en esferas concéntricas. En el centro del Cosmos se encontraba la Tierra sometida a procesos de generación y corrupción y sucesivamente la esfera de la Luna; la de Mercurio, la de Venus, la del Sol, hasta la esfera más externa de las estrellas fijas. Este mundo finito acotado por esferas, estructuraba el espacio, le daba orden y lo jerarquizaba desde el mundo sublunar, sometido a fenómenos de generación y corrupción, hasta alcanzar la perfección de las estrellas fijas. Fuera de las esferas fijas del cielo, estaba la Casa de Dios.
Los fenómenos físicos en el mundo Ptolemaico-Aristotélico se desarrollaban dentro del mundo sublunar. En este mundo el movimiento local era un estado transitorio. Además, en el mundo sublunar solamente existía un movimiento local natural que era el movimiento vertical, por el cual, los cuerpos pesados (compuestos por los elementos agua y tierra) tendían a moverse hacia la Tierra (hacia abajo) y los cuerpos más ligeros (formados fundamentalmente por aire y fuego) hacia arriba. Los cuerpos se movían para alcanzar el único estado permanente de los cuerpos, que era el reposo.
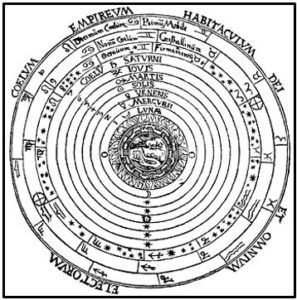
En un Cosmos cerrado, como el Ptolemaico-Aristotélico, con movimientos naturales acotados y definidos, el papel de la Geometría era escaso; el estudio del movimiento se basaba en lo que nos decían nuestros sentidos. Con la destrucción del mundo finito y estructurado y la adopción del espacio geometrizado de la ciencia moderna se pasaba de mundo finito y ordenado a otro mundo infinito, sin orden y sin centro que no estaba unificado por su estructura, sino por las leyes que regían sus movimientos.
El estudio del movimiento en la Ciencia Moderna se basa en unos principios que contribuyeron a abandonar la concepción de un mundo cerrado y adoptar la idea de un espacio infinito. El supuesto más importante de la Ciencia Moderna para llegar a abandonar el espacio cerrado fue el de considerar que el movimiento era un estado permanente igual que lo era el reposo y la ley fundamental del movimiento era el Principio de Inercia, que reproducimos en la formulación cartesiana según la formuló R. Descartes (1596-1650) en los Principios de Filosofía (1644).
Descartes afirmaba que Dios había creado la materia dotada de dos estados permanentes: de movimiento y de reposo. Además, Dios había dotado a la materia de una ley de la persistencia que decía que la cantidad de materia y la cantidad de movimiento, una vez creados, permanecen constantes eternamente. Descartes, además de dar una explicación teológica del movimiento, formuló unas leyes de la naturaleza del mismo que fueron aceptadas por I. Newton (1642-1727).
Ley 1.- (Persistencia o perseverancia de los estados) Cada cosa persevera siempre en su estado; y así, lo que es movido una vez continúa moviéndose siempre, permanece en el mismo estado y nunca puede cambiarse sino por causas.
Ley 2.- (La tendencia de los cuerpos en movimiento a seguir trayectorias rectilíneas) Ninguna de las partes de la materia, considerada en sí misma, tiende a continuar moviéndose en línea curva, sino solamente en línea recta.
Newton formuló esta Ley de Inercia en los Principia (1687): Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser en tanto sea obligado por fuerzas impresas a cambiar de estado.
La Ley de Inercia está en relación directa con el concepto de reposo absoluto en el espacio infinito inmóvil, según se sigue de su explicación del fenómeno gravitacional:
Una piedra volteada en una honda intenta escapar de la mano del hondero y su intento hace estirarse la honda y más cuanto más rápidamente gira, y, en cuanto se suelta se aleja. Llamo centrípeta a la fuerza contraria al mencionado intento; por ella, la honda retiene constantemente la piedra hacia la mano y la mantiene en el círculo y, por tanto, se dirige hacia la mano o hacia el centro del círculo. Igual ocurre con todos los cuerpos que giran en círculo. Todos intentan alejarse del centro y a no ser por una fuerza contraria a este intento, que los cohíba y los obligue en sus órbitas, y a la que por ello llamo centrípeta, se alejarían todos en línea recta con movimientos uniformes.
En este pasaje de los Principia, Newton describía el movimiento inercial en línea recta al infinito en cuanto la fuerza dejaba de ser ejercida.
La explicación de la Ley de Inercia en la mecánica newtoniana se justificaba por la existencia de un espacio sin resistencia, donde los cuerpos, una vez que dejaba de actuar la fuerza que los impulsaba, continuaban moviéndose indefinidamente, siempre en línea recta, para lo que es necesario un espacio infinito compatible con la Geometría de Euclides y no finito y confinado como describía el Cosmos Ptolemaico-Aristotélico.