Una de las consecuencias de la Teoría de la Relatividad, debido a la dilatación del tiempo, es la contracción de la longitud en la dirección del movimiento de los cuerpos que viajan a velocidades cercanas a la de la luz. Dicho de otra forma: Cuando se mide la longitud de un objeto desde un Sistema de Referencia que se mueve respecto al objeto será siempre menor que la longitud característica de ese objeto, es decir, será menor que la longitud medida desde el sistema de referencia del objeto. La contracción se da en la dirección del movimiento del cuerpo.
Analizaremos el problema de dos observadores, A (situado dentro del vagón) y B (que está en el andén), que miden la longitud de un vagón que se desplaza por una vía rectilínea a una velocidad v:
El observador A mide la longitud desde dentro del vagón con un reloj de luz y el siguiente procedimiento. Emite un rayo de luz desde la parte trasera del vehículo, M, la luz se refleja en un espejo situado en la parte delantera, N, y se refleja en un espejo hasta alcanzar el foco emisor. El observador A ha medido la longitud del vagón, L0 , y comprueba que la luz invierte, en el recorrido de ida y vuelta, un tiempo Δt0, Por tanto, como la velocidad de la luz, c, es constante en cualquier sistema de referencia y para recorrer la longitud 2L0 ha empleado un tiempo Δt0, se tiene que
c = 2·L0/Δt0
El observador B situado en el andén mide la que debe medir la longitud observando el momento de emisión del rayo luminoso, el de su llegada al espejo en la parte delantera y su llegada al foco emisor, para lo que invierte un tiempo Δtm para recorrer la longitud 2Lm, (Lm es la longitud de vagón medida desde el andén) esta longitud la puede determinar porque la velocidad de la luz, c, es constante en cualquier sistema de referencia y verificará que
c = 2Lm /Δtm
Por lo tanto podemos escribir que:
c = 2L0/Δt0 = 2Lm/Δtm
donde Δt0 y Δtm son los intervalos de tiempo que mide cada observador que se tarda en recorrer la longitud correspondiente. De aquí obtenemos que:
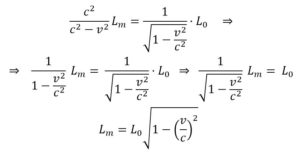
Lm = L0 · Δtm/Δt0 o Lm /L0 · Δtm/Δt0 (1 )
y como Δtm = γ·Δt0, es decir:
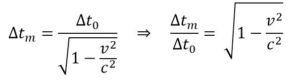
De (1) obtenemos que:
L0 medirá el tiempo propio del vagón que es una magnitud fundamental en relatividad que se define como el tiempo que mide un reloj unido a un objeto en movimiento arbitrario; es una propiedad absoluta del movimiento del objeto, y por tanto, del reloj en ese movimiento y como:
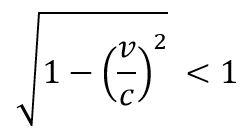Entonces, Lm < L0 lo que indica la contracción de la longitudes de los cuerpos en movimiento en la dirección del movimiento es menor que el tiempo la longitud que se mide acompañando al movimiento.
También se puede calcular teniendo en cuenta la adición de velocidades y la ecuación de la dilatación de tiempo. Para ello cuando la luz recorre el vagón de M a N B observa que lleva una velocidad c – v y cuando vuelve de N a M observa una velocidad de c + v, con lo cual estima un tiempo de
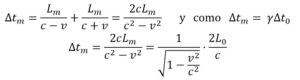
Por lo tanto:
