
La palabra criptografía procede del griego (cryptós, que significa oculto y graphein, que quiere decir escribir). Un criptograma será, por tanto, un mensaje oculto escrito, esto es un mensaje secreto. Cuando un mensaje nos parece incomprensible o indescifrable decimos que es críptico. Uno de los criptogramas más famosos de la literatura se encuentra en el relato corto de Conan Doyle Los Bailarines.
Cuando tenemos un mensaje encriptado para saber lo que dice tenemos que conocer la clave. En los criptogramas aritméticos que voy a presentar sólo hace falta conocer los algoritmos de las operaciones aritméticas.
PRIMERO – En la siguiente suma cada letra es una cifra, en la que G ≠0. Se pide sustituir cada letra por una cifra para que la suma indicada sea correcta
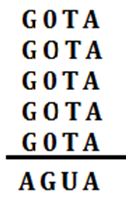
SOLUCIÓN: Razonaremos de la siguiente forma:
1.- Sumando las unidades A+A+A+A+A = 5A, que es un número que termina en la cifra A. Como todo número multiplicado por 5 acaba en cero o en cinco, necesariamente A tiene que ser cero o cinco.
2.- A no puede ser cero, porque si no también G sería cero, luego A = 5
3.- G debe ser igual a 1. Ya que 5G mas las que se lleven de sumar O+O+O+O+O deben ser 5. Además 5·O no se lleva nada y como no puede ser 1, porque G=1 y G ≠A = 1, entonces O debe ser cero
4.- La T tiene que ser un 2 o un 3 tenemos que T+T+T+T+T tiene que tener una decena [G=1 y O = 0]. Si T = 2, como llevamos dos decenas de A+A+A+A+A, U también será 2 y no puede ser, porque suponemos que T=2. Si T=3, la U =7, luego el resultado es:
GOTA =1035 y AGUA = 5175 .
SEGUNDO.- En el siguiente producto cada letra es una cifra. En la que A ≠0. Se pide sustituir cada letra por una cifra para que el producto indicado sea correcto.
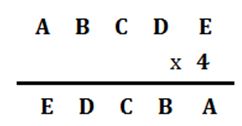
SOLUCIÓN
- A tiene que ser 1 o 2 (si fuera mayor que 2 el producto tendría seis cifras y no puede ser 1 porque 4E (producto de las unidades por cuatro da A y , por lo tanto, A tiene que ser par, luego A = 2.
- Si A =2, E tiene que ser 8 o 3 (que multiplicado por cuatro da 32 y 12 respectivamente), pero no puede ser 3 porque A = 2 y E debe ser mayor o igual que 8, por tanto E = 8
- 4B < 10 , luego B tiene que ser un o dos, como A=2 implica B=1.
- Como 4·E = 32, 4D+3 tiene que acabar en 1 luego D = 2 o 7, pero A=2, luego D=7.
- Como 4D +3 =31, 4C+3 tiene que acabar en C luego C =9. La solución será:
21978x4=87912
TERCERO .- En la siguiente suma cada letra es una cifra. Se pide sustituir cada letra por una cifra para que la suma indicada sea correcta.

SOLUCIÓN
- Observando la suma de las unidades I+I+I+ I+ I = 5·I acaba en 0 o en 5
Si I = 0 , 5·S = 10 A + S ⇒ 4S = 10A ⇒ 2S = 5A ⇒ S= 5 A=2
50+50+50+50+50 = 250
Si I =5 , 10 A + S = 5S+2 ⇒ – 4S +10 A = 2 ⇒ -2S + 5A = 1
A=(1+2S)/5 S = 2 A = 1
25+25+25+25+25 = 125
CUARTO.- En la siguiente suma cada letra es una cifra. Se pide sustituir cada letra por una cifra para que la suma indicada sea correcta.

SOLUCIÓN
- Fijándonos en la cifra de los millares O sólo puede ser 1,2 o 3, pero, observando las¡la cifra de las unidades, como O tiene que ser par, por ser 4·S múltiplo de 4, entonces, O debe ser par y, por tanto O=2
- Como O = 2, S sólo puede ser 3 u 8.
- Si S = 3 entonces H =9, lo que nos da para D las posibilidades D= 5 y C=0, D = 6 y C=4 , D =7 y C = 8 y D = 8, C=2, que no puede ser (ya que O =2). Son soluciones:
523+523+523+523 = 2092 623+623+623+623 = 2492 723+723+723+723 = 2892
4. Si S = 8 entonces H = 1, lo que nos da para D las posibilidades D= 5 y C= 1 (no C = H= 1), D = 6 y C=5 , D =7 y C= 9 y D= 9, C = 8 , (No, S =8). Son soluciones
628+628+528+528 = 2512 728+728+728+728 = 2912

