
Es difícil entender cómo el descubrimiento de las magnitudes inconmensurables desencadenó una crisis en la matemática griega, pero gracias a ese hallazgo el razonamiento matemático afinó sus métodos de análisis y, aunque obligó a dejar de lado lo infinitamente grande y lo infinitamente pequeño, contribuyó a proporcionar a la matemática un lenguaje riguroso y sin contradicciones que la habría de coronar como la reina de las ciencias
La visión atomista de la Naturaleza de Leucipo (siglo V a. de J.C.) y de Demócrito (480-370 a. de J.C.) recibió un duro golpe cuando en la Escuela Pitagórica, a comienzos del siglo, descubrieron que existían pares de magnitudes que no podían ser medidas con la misma unidad, o, lo que es igual, que había magnitudes que no podían ser comparadas de forma exacta y precisa.
Las magnitudes matemáticas estaban formadas por unidades, si eran aritméticas por repetición de la unidad, si eran geométricas las unidades debían ser puntos y si eran físicas por átomos, por lo tanto, se creía que las magnitudes debían estar formadas por un cierto número de elementos y, en último término, tenían que tener una unidad de medida común, ya fuera unidad, punto o partícula atómica indivisible.
El descubrimiento de magnitudes no comparables fue una sorpresa porque contradecía el sentido común. Las magnitudes estaban formadas por unidades de debían poder comparar. Pero los Pitagóricos demostraron que entre el lado y la diagonal del cuadrado y entre el lado y la diagonal del pentágono no podía existir una unidad de medida, por pequeña que fuese, capaz de expresar la medida de ambas mediante sendos números enteros.
A continuación probaremos que el lado y la diagonal del pentágono son magnitudes no comparables y procederemos por reducción al absurdo
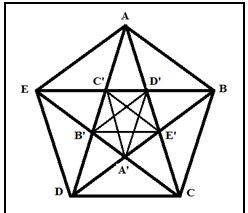
Si la unidad u midiera al lado AB y a su diagonal AC, como ABE’ es un triángulo isósceles, AB = AE’ y la unidad u mediría a E’C y a AD’ y por consiguiente (como BCD’ es un triángulo Isósceles igual a ABE’), la unidad u medirá también a E’D’ que es el lado del pentágono interior, ya que
E’D’ = AC – E’C – AD’
Por otra parte, E’C y AD’ son iguales a las diagonales del pentágono interior A’B’C’D’E’ (ya que, por ejemplo, CB’E’ es isósceles) y se tiene que la unidad u que medía el lado y la diagonal del pentágono ABCDE mide también el lado y la diagonal del pentágono interior A’B’C’D’E’. El proceso no acaba nunca y esto viene a demostrar la no existencia de tal unidad común.
El descubrimiento de magnitudes inconmensurables trastocaba el orden finitista pitagórico para el que todo procedía de la unidad y, por lo tanto, la creencia que todo se podría explicarse a partir de la unidad. En la aritmética la unidad de medida común entre dos magnitudes se podía calcular por el máximo común divisor de dos números (mediante el algoritmo de Euclides, por ejemplo), pero ese mismo procedimiento para hallar una unidad de medida común fallaba en la Geometría.
Si se aceptaban los procesos infinitos de división como el utilizado en Geometría, al dividir una recta sucesivamente, en un número infinito de partes, cada una de ellas no tendrá ninguna magnitud. Las rectas continuas no estarán formadas por puntos, ya que los puntos geométricos no debían ocupar un lugar real, ya que por muchas partes que se puedan hacer de una recta nunca se llega a uno.
Este descubrimiento dio lugar a varios temas centrales en el estudio de las matemáticas y que me limito a enumeraremos para tratarlos más adelante, en primer lugar, la relación entre magnitudes inconmensurables abrió la puerta a los números irracionales. En segundo se eliminaron de las matemáticas el infinito y los procesos infinitos y, finalmente, se abordó el problema de la comprensión del continuo físico y del continuo matemático y sus paradojas relaciones.
Aristóteles dio una solución al manejo del infinito introduciendo las nociones de infinito actual y de infinito potencial. Considera el infinito potencial como un proceso de crecimiento indefinido o de divisiones sin final, que en el caso de las matemáticas será la tendencia hacia lo más grande y hacia lo más pequeño. Se basa en la operación reiterativa e ilimitada; dado un número natural siempre podemos concebir otro mayor, y otro aún mayor y así sucesivamente sin que lleguemos nunca a tener el conjunto infinito. El tratamiento en Matemáticas de conjuntos infinitos como entidades reales comenzó en matemáticas con los trabajos de B. Bolzano (1781-1848) y de G. Cantor (1845-1904). El infinito actual fue desterrado de la matemática griega.
El descubrimiento de las magnitudes inconmensurables está asociado a una historia que entra en mundo de la leyenda. Cuenta que Hipaso de Metaponto fue arrojado al mar por los de su secta: los Pitagóricos por haber difundido fuera de la Hermandad el descubrimiento de los irracionales. Hipaso, hacia el año 450 a.C., descubrió las magnitudes inconmensurables, las cuales tenían relaciones geométricas que no eran expresables en forma de fracción. El descubrimiento tuvo tanta repercusión que marcó la historia del pitagorismo y la historia de las matemáticas en Grecia.
El historiador Jámblico (245-325) escribió en su libro Vida de Pitágoras la historia (ocho siglos después) dela siguiente forma:
Hipaso era un pitagórico, pero al haber divulgado por escrito como se podía construir una esfera a partir de doce pentágonos, pereció en el mar por haber cometido ese acto de impiedad. Recibió el mérito por ese descubrimiento pero en realidad todo provenía de ÉL”.
Él era Pitágoras y los descubrimientos de su Escuela se le atribuían todos a él y debían permanecer en secreto y el secreto del pentágono cuestionaba el principio pitagórico de que la unidad era el origen de todo. El pentágono encerraba las maravillas de la belleza (número áureo), pero también ocultaba la irracionalidad.
