
PROBLEMA 1 .- Se desea construir un edificio de planta circular en terreno de forma circular y dejar el edificio rodeado de una zona ajardinada en forma de media luna como muestra la figura (en amarillo), pero no se conocen los radios de los círculos que delimitan el jardín, no obstante se han tomado las medidas de 10 y 18 m que se indican en la figura . ¿Cuál es la medida de los radios de los círculos y cuánto mide la zona destinada a jardín?
Respuesta. Sean R y r los radios del círculo mayor y del menor respectivamente: de la figura se desprende que 2R -2r = 18 ⇒ R -r =9 ⇒ R = r + 9 m
Por otra parte, aplicaremos la propiedad que tienen los ángulos inscritos en una circunferencia y es que su mecida es igual a la medida de la mitad del arco que abarcan sus lados.
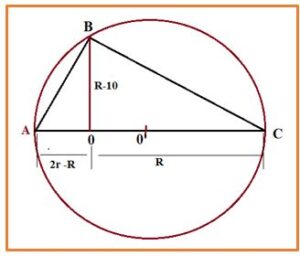
Consideremos el triángulo extraído de la figura construida sobre la planta del edificio que se desea construir, en la que el triángulo ABC es rectángulo en B y el segmento BO es la altura relativa a la hipotenusa. La altura relativa a la hipotenusa es media proporcional entre los segmentos que determina sobre ella.
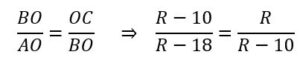
R2 – 20 R + 100 = R2 -18R ⇒ 2R =100 ⇒ R = 50 m y r = 41 m
Área de la zona ajardinada = 502 – 412 = 819 m2 .
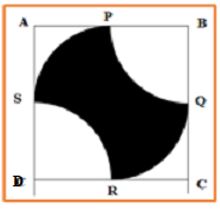
PROBLEMA 2.- En un cuadrado ABCD de lado 2 m , se trazan desde los vértices B y D dos cuadrantes de circunferencia, PQ y SR y desde el centro del cuadrado otros dos cuadrantes SP y RQ resultando la figura PQRS, dibujada en negro ¿Cuál es el área de PQRS?
Respuesta:
Area PQRS = Area ABCD -2 Area PBQ – 2 Area PAS =
= 4 – [2( π/4) ]- [2 (1- π/4)] = 2 m 2
La figura siguiente ofrece un aspecto gráfico, considerando el cuadrado PQRS de lado √2 y un mosaico Nazarí

PROBLEMA 3.- Sean dos círculos concéntricos de radios R y r respectivamente tales que una secante del círculo mayor es tangente al círculo menor y mide tiene longitud 10 cm, ¿Cuál es el área del anillo circular?
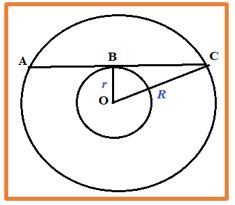
Respuesta: Observemos que la secante AC, que tangente al circulo menor en el punto medio B determina el triángulo rectángulo en OBC, que cumple:
BC2 = OC2 + OB2 ⇒ 25 = R2 – r2
El Area del anillo es :
π R2 – π r2 = π (R2 – r2) = 25 π cm2 .
PROBLEMA 4.- Se amarra una cinta alrededor del ecuador de la tierra y otra alrededor del perímetro (ecuador) de la luna (suponiendo que tanto la tierra como la luna tienen una forma esférica perfecta ). Supongamos que ambas cintas se separan un metro de la superficie todo lo largo del perímetro. Sea A la cantidad de cinta que hay que añadirle a la cinta de la tierra y B la cantidad de cinta que hay que añadirle a la cinta de la luna para que se cierren. ¿ Qué proporción hay entre A y B ?.
Respuesta: La cinta de la Tierra medirá: 2πRT (Supongamos que RT está expresado en metros). Si queremos separar la cinta 1 m de la superficie le añadimos A, entonces su longitud será: 2π(RT+1) y entonces: 2π(RT+1) – 2πRT = A ⇒ A = 2π
Análogamente la cinta de la Luna medirá: 2πRL (Supongamos que RL está expresado en metros). Si queremos separar la cinta 1 m de la superficie le añadimos B, entonces su longitud será: 2π(RL+1) y entonces 2π(RL+1) – 2πRL = B ⇒ B = 2π
La relación es 1.




