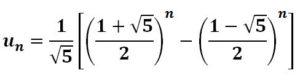
El cálculo matemático presenta algunas veces verdaderas sorpresas. A continuación voy a mostrar como una serie de expresiones de aspecto complicado, porque en ellas aparecen radicales y potencias elevadas , se reducen a números enteros. Es lo que sucede con el término general de la sucesión de Fibonacci:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
en la que cada término de la misma se obtiene sumando los dos anteriores y que, aunque está formada por números enteros, tiene por término general una expresión en función de potencias de radicales de una forma tan imponente como:
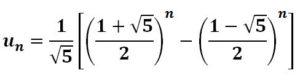
Dando a n en esta expresión los valores 1, 2, 3, 4,… se obtiene la sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…
A continuación hacemos un esbozo de por qué sucede esto:
1.- Una sucesión numérica de números reales es un conjunto ordenado de números. La representación general de una sucesión es:
a1, a2, … , an, an+1, …. ,
donde el subíndice indica el número de orden que ocupa cada número en la sucesión. Así, el número a2 ocupa el segundo lugar y an está en enésima posición.
Ejemplos de sucesiones:
- En la sucesión 2, 4, 6, 8, 10, 12…. el término a4 = 8 y el a6 = 12
- En la sucesión 2, 5, 8, 11, 14, 17…. el término a2 = 5 y el a5 = 14
2.- Se llama término general de una sucesión a una expresión an = f(n) (que depende de n) tal que cuando n toma el valor 1 obtenemos a1, si si toma el valor 2 obtenemos a2 y así sucesivamente.
Ejemplos
- La sucesión 2, 5, 8, 11, 14, 17…. tiene el término general an = f(n) = 3n-1
- La sucesión 3, 8, 15, 24, 35, 48,… tiene el término general an = f(n) = n2 +2n
3.- Una sucesión se llama recurrente cuando cada término de ella está definido en función de los anteriores; y los primeros (llamados valores iniciales) están definidos
Ejemplo: La sucesión un+1 = 2 u n es recurrente, ya que cada término se expresa en función de su inmediatamente anterior. Calcularemos su término general para el valor inicial u1 = 5
u2 = 2 u1
u3 = 2 u2
………….
u n = 2 u n-1
Multiplicando los primeros miembros entre si, igualándolos al producto de los segundos miembros y simplificando resulta u n = 2n-1 u1 , que imponiéndole el valor inicial u1 = 5, resulta que el término general es u n = 5 ·2n-1
Podemos escribir la sucesión 5, 10, 20, 40, 80. …
Observación: Para resolver ecuaciones recurrentes homogéneas como la anterior: u n+1 – 2 u n = 0, con una condición inicial u1 = 5, en la práctica se prueban soluciones de la forma: un = r n y sustituyendo en u n+1 – 2 u n obtenemos:
r n+1 – 2r n = r n (r – 2) = 0 ⇒ r = 0 (trivial) y r =2 , lo que significa que :
un+1 = 2·2 n = 2n+1 , y,
como la ecuación es homogénea, las soluciones serán del tipo
un = A 2n
Para calcular el valor de la constante A sustituiremos el valor inicial, u1 = 5 en
un+1 – 2 u n = 0 ⇒ u2 – 2 u1= 0 ⇒ A 22 – 2 · 5 = 0 ⇒
⇒ A = 5/2 ⇒ un = (5/2) 2n ⇒ u n = 5 ·2n-1
Este tipo de soluciones se utilizan pra resolver ecuaciones recurrentes homogéneas de orden superior como:
Ecuaciones recurrentes homogéneas de orden 2 :
an u n + an-1 un-1 + an-2 u n-2 = 0
Un ejemplo de estas sucesiones recurrentes de segundo orden es la sucesión de Fibonacci en la que cada término de la sucesión es suma de los dos anteriores, por lo tanto para calcular su término general tendremos que disponer de la ley de recurrencia y de los valores numéricos de los dos primeros términos:
u n+2 = u n+1 + u n , con valores iniciales u1 = 1 y u2 = 1
la sucesión la podemos escribir en la forma:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Para hallar su término general buscaremos soluciones del tipo un = r n, sustituyendo en la ecuación de recurrencia:
u n+2 = u n+1 + u n ⇒ r n+2 = r n+1 + rn
⇒ rn ( r2 – r – 1 ) = 0 ⇒ r2 – r – 1 = 0
Resolviendo la ecuación de segundo grado obtenemos las dos soluciones:
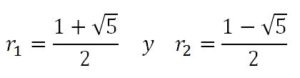
Como la ecuación es homogénea, la solución general será de la forma:
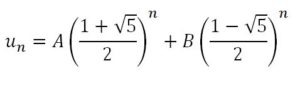
Calculando A y B con los valores iniciales: u 1 = 1 u 2 = 1 enel sistema de ecuaciones siguiente :
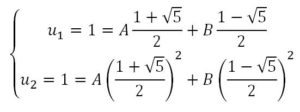
Resolviendo el sistema de obtiene:
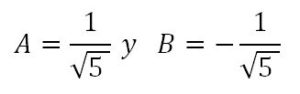
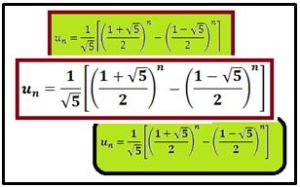
Por lo tanto, la expresión del término general que para cada valor de n nos proporcionará un número entero será: