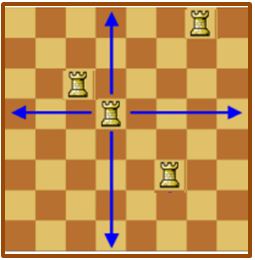
El ajedrez ha sido y sigue siendo una fuente constante de problemas y pasatiempos matemáticos. Problemas sobre los saltos del caballo o para determinar el número de damas, alfiles o torres que se pueden colocar en un tablero sin que se amenacen son cuestiones que se han planteado en los libros de matemáticas y a los que han dedicado su atención grandes matemáticos.
En este escrito vamos a dedicarnos a reflexionar sobre algunas particularidades del movimiento y las posiciones de la torre en el tablero a través de las siguientes cuestiones.
Problema 1.- ¿De cuántas formas se pueden colocar ocho torres en el tablero de ajedrez de manera que no se ataquen mutuamente?
Solución: Para que no se amenacen, cada torre debe ocupar una fila y una columna distinta de las demás, es decir, no puede haber dos torres en la misma fila ni en la misma columna.
Para determinas las psiciones posibles pensemos que para colocar la primera de las ocho torres sin que se amenacen comenzamos con la columna a y podemos elegir cualquiera de las ocho filas numeradas de 1 a 8. Para colocar la segunda torre tomamos la columna b y podemos elegir cualquiera de la siete filas restantes (cualquiera menos la que hayamos seleccionado sobre la columna a). Para colocar la tercera tomamos la columna c y podemos elegir entre las seis filas restantes (cualquiera menos las que hayamos seleccionado sobre las columnas a y b) y así sucesivamente, por tanto, recorriendo las ocho columnas las torres se pueden colocar de
8·7·6·5·4·3·2·1 = 8!= 40.320
formas posibles
Problema 2.- ¿De cuántas formas distintas se pueden colocar ocho torres en un tablero de ajedrez de forma que al menos dos de ellas se amenacen entre sí?
Solución: El número total de formas en las que se pueden colocar ocho torres en un tablero 8×8 serán:
De esta cantidad, por el problema anterior, habrá que restar las 40.320 formas de colocar las torres de manera que no se amenacen entre sí, Como el número de formas posibles de colocar las ocho torres es 4.426.165.368, habrá
tales que dos de ellas al menos se amenacen entre si.
Problema 3.- Numeramos las casillas de un tablero de ajedrez del 1 al 64 de la siguiente manera: la primera fila, con los números del 1 al 8, de izquierda a derecha; la segunda fila, con los números del 9 al 16, de izquierda a derecha, y así sucesivamente. Si se colocan en el tablero ocho torres de modo que no se amenacen unas con otras. ¿Cuál es la suma de los números de las casillas que ocupan las torres?
Para resolver el problema tendremos en cuanta las siguientes consideracione
1.- Cada casilla vendrá determinada por dos coordenadas (a, b), la primera indica la columna y la segunda la fila. Así, con abuso de lenguaje, diremos que (2, 3) = 18 o que (6, 5) = 38
2.- La solución pasa por considerar que para que dos torres no se coman, la segunda torre no puede estar ni en la fila ni en la columna cubierta por la otra.
3.- La suma de los elementos de las diagonales será:
Diagonal 1: 1 + 10 + 19 + 28 + 37 + 46 + 55 + 64 =
= 8(1+64)/2 = 260
Diagonal 2: 8 + 15 + 22 + 29 + 36 + 43 + 50 + 57 = 8(8+57)/2 = 260
Daremos una idea de la demostración para probar que la suma de los números de las casillas que ocupan las ocho torres cuando no se amenazan entre sí será siempre la misma, esto es, 260.
Veremos que cada una de las 40.320 posiciones posibles en que las torres no se amenazan entre sí, se puede transformar en otra de ellas cuyas posiciones tengan la misma suma, pero con una torre más en la Diagonal 1.
Si una de las torres ocupa la posición (a, b), a ≠ b , entonces, pensemos por filas:
[Supongamos que a > b] Si desplazamos (a, b) = m (en nuestra figura (7, 2) = 15) hasta la posición de la diagonal (b, b) = n (en nuestro caso (2, 2) = 10) la suma habrá disminuido a – b = m-n unidades (en nuestro caso7 – 2 = 15 – 10 = 5).
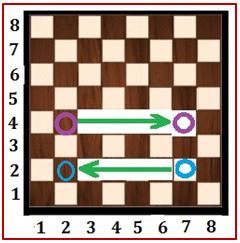
Pero la torre desplazada al lugar (b, b) se verá amenazada por otra torre de la posición elegida que estará su misma columna, (b, b’), que podemos desplazarla por su misma fila a – b unidades hacia la derecha los que obtenemos otra posición (a, b’) con la misma suma que la de partida, pero con un elemento más en la diagonal.
Resumiendo: La torre situada en (a, b) se desplaza |a – b| unidades hasta (b,b) que amenaza a otra reina colocada en (b, b’), la cual se desplaza |a – b| unidades en sentido opuesto al anterior hasta al lugar (a, b’)
El proceso se puede repetir sucesivamente, hasta que todas las torres estén en la diagonal 1. Por lo tanto la suman, cuando numeramos el tablero de la gorma indicada i sumamos las números de la posiciones de las ocho torres cuando no se amenazan sumarán 260.
El problema puede generalizarse para cualquier tablero cuadrado de lado n y la respuesta es que la suma de las posiciones de las torres será n (n2 + 1) / 2.
