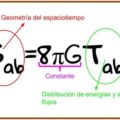
Aristarco de Samos (320-250 AC) fue, seguramente, el primer astrónomo que propuso el modelo heliocéntrico del universo y realizó la primera estimación de la relación entre distancias de la Tierra (T) a la Luna (L) y la distancia de la Tierra al Sol (S),
Observó que, cuando la Luna tenía iluminada justamente a la mitad del círculo, el Sol, la Luna y la Tierra formaban un triángulo rectángulo (TLS rectángulo) con el ángulo recto situado en la Luna.
Midió el ángulo LTS unos 87º, por tanto:
Si DL es la distancia Tierra-Luna y Ds es la distancia Tierra-Sol se tiene que:
DL/Ds = cos 87º = 0,053 ⇒ Ds ≈ 19,1·DL.
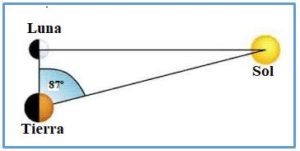
Si DL es la distancia Tierra-Luna y Ds es la distancia Tierra-Sol se tiene que: DL/Ds = cos 87º = 0,053 ⇒ Ds ≈ 19,1·DL.
Es decir, que la distancia de la Tierra al Sol era unas veinte veces mayor que la distancia de la Tierra a la Luna. Como ambos tienen el mismo diámetro aparente (medio grado), el Sol ha de ser 20 veces mayor que la Luna.
En ese momento de la historia no se conocía ninguna distancia de las dos distancias, por tanto, sólo se obtuvieron relaciones. Pero tuvo una gran importancia Eratóstenes de Cirene (276 a.C-194 a.C.) que midió el radio de la Tierra, al que estimó en 6.300 km.
El primero en abordar el cálculo de la distancia a la Luna fue Aristarco de Samos a partir de los datos obtenidos durante un eclipse de Luna. El método de Aristarco fue mejorado un siglo más tarde por Hiparco de Nicea (190-120 a. C.) utilizando la medida del radio de la Tierra realizada por Eratóstenes. Hiparco concluyó que la distancia entre la Luna y la Tierra era, aproximadamente, treinta veces el diámetro de ésta y como, según Eratóstenes el diámetro de la Tierra era de 12.600 kilómetros, la distancia entre la Luna y la Tierra debía ser de 378.000 km, una medida de una precisión asombrosa
La observación que se realizó durante el eclipse de Luna fue el siguiente constató que el satélite empleaba una hora desde que contactaba en la zona de sombra, hasta que desaparecía completamente en la sombra.

Luego observó que tardaba 3,7 horas en volver a salir completamente de la zona de sombra. Y concluyó que el diámetro de la sombra de la Tierra era casi cuatro veces el diámetro de la Luna. Él pensaba que el diámetro de la Tierra era igual al diámetro de su sombra, suposición que era admisible y ciertamente aproximada, considerando la enorme distancia al Sol a la Tierra. Por tanto, concluyó que el diámetro de la Tierra era 3,7 veces el de la Luna.

Una vez conocido el tamaño real de la Luna, 3.505 km, es fácil calcular la distancia a la que se encuentra de la Tierra a partir del ángulo bajo el que se ven los bordes más separados de la circunferencia que la limita. Este ángulo es de α = 0,51º. Entonces la forma de calcular la distancia a Tierra, o, lo que es lo mismo, el radio de su órbita, se obtiene mediante la siguiente proporción:
Si al diámetro de la Luna (α = 0,51º) le corresponden 3405 Km., a 360º le corresponde la longitud de la órbita lunar (2·π·RL). El radio RL de la órbita es la distancia entre la Luna y la Tierra.

Lo que constituye una estimación magnífica de la medida real .
Volvemos con Aristarco para concluir una historia que duró casi dos siglos de preocupaciones, especulaciones y mediciones. Aristarco a comienzos del siglo III observó que Ds ≈ 19,1·DL, que era una relación alejada de la realidad, pero obtenida con un método impecable. El error procedía de que el ángulo LTS (Luna-Tierra-Sol) no es de 87º, sino de 89º 51’, es decir, casi un ángulo recto, y no era posible esperar mucha más precisión con los rudimentarios instrumentos que manejaban los primeros astrónomos hace veinticuatro siglos. Medio siglo después Eratóstenes midió con una precisión extraordinaria el radio de la Tierra, que estimó en 6300 km. Resultado que fue utilizado por Hiparco que había obtenido, en la observación de un eclipse de Luna que la distancia entre la Luna y la Tierra era, aproximadamente, treinta veces el diámetro de ésta. Por tanto, Distancia Tierra- Luna era DL = 30·12600 = 378.000Km lo que suponía una precisión extraordinaria.
Pero la relación de Aristarco Ds ≈ 19,1·DL, que metía por medio la medida del ángulo que LTL = 87º, implicaba que Ds = 19,1 · 382727 = 7.310.085 Km, que es un número muy alejado de la medida real debido las razones anteriormente señaladas.