El Libro II de los Elementos de Euclides contiene lo que se ha dado en llamar Álgebra Geométrica. En realidad en el Libro no se estudian ecuaciones y ni siquiera se resuelven problemas numéricos, sino que se ocupa de estudiar relaciones entre áreas de rectángulos y de cuadrados. Sin embargo, sus proposiciones establecen relaciones e identidades entre las áreas de las figuras que tienen una fácil traducción al lenguaje algebraico.
Los matemáticos árabes realizaron la labor de traducción de las proposiciones del Álgebra Geométrica al lenguaje numérico y algebraico. En particular, fue decisiva la obra del matemático Al-Khwarizmi (780-850) en su obra Kitab al-jabr wa al-muqabalah. La obra fue traducida por primera vez al latín, y por tanto conocida en occidente por Adelardo de Bath (1090-1160), en la Escuela de Traductores de Toledo en 1120 y su influencia en las matemáticas de la época fue enorme. A través de esta obra se unen dos corrientes: la notación numérica indo-arábiga y la tradición geométrica griega. La traducción del título de la obra de Al-Khwarizmi era complicada (el término jabr indica la operación de pasar un término al otro lado del signo igual de una ecuación y la palabra muqabalah significaba la simplificación de términos iguales) por lo que el traductor Adelardo y traductores posteriores latinizaron el título, llamándolo aljeber que acabó evolucionando a álgebra. Una muestra más de la importancia de la obra es que la palabra algoritmo, tan utilizada en matemáticas, deriva del propio nombre del autor: Al-Khwarizmi.
En las Universidades Medievales en la Facultades de Filosofía se estudió el Álgebra Geométrica de Euclides y se utilizó para resolver ecuaciones de segundo grado. El aragonés P. Sánchez Ciruelo (1470-1548), profesor de Teología y Astronomía en las universidades de París, Alcalá y Salamanca, publicó en 1516 la obra Cursus quattuor Mathematicarum Artium Liberalium (Las cuatro artes liberales formaban los estudios del Quadrivium: Aritmética, Astronomía, Geometría y Música), en la que recopiló los métodos de la Geometría Griega, así como la numeración indo-arábiga, el Álgebra de los matemáticos musulmanes y de otros autores europeos como J. Sacrobosco (1195–c.1256), L. de Pisa (1175-1240) o Th. Bradwardine (1290 – 1349) formando un obra amplio compendio de Matemáticas, en el que incluyó un amplio capítulo de resolución de ecuaciones de segundo grado con métodos fundamentados en la Geometría.
a) (b – x)·x = c2. (equivalente: – x2 = – bx + c2 o x2 + c2 = bx )
b) (x – b)·x = c2. (responde a: x2 – bx = c2 o x2 = bx + c2 )
c) (b + x)·x = c2 (responde a: x2 + bx = c2).
Resolveremos mediante los métodos del Algebra Geométrica la ecuación cuadrática tipo:
a) (b – x)·x = c2.
Para ello se utilizaba la Proposición 5 del Libro II de los Elementos de Euclides que dice:
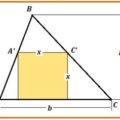
Proposición 5: Si se divide un segmento en partes iguales y desiguales mediante dos puntos M y D, el rectángulo determinado por las partes desiguales, más el cuadrado de la de lado la distancia entre los dos puntos que dividen la recta es igual al cuadrado de la mitad de la recta dada.
Algebraicamente la podemos escribir de la siguiente forma: si tenemos un segmento AB y un punto D divide a AB en dos segmentos desiguales AD = p y DB = q y que otro punto M divide a AB en dos partes iguales, que tendrán la longitud AM = MB = (p+q)/2. Luego la Proposición 5 se puede escribir de forma algebraica de la forma siguiente:
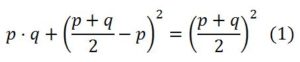
Cuya validez se puede comprobar de forma algebraica y la emplearemos para resolver la ecuación:
(b – x)·x = c2.
Sean AB un segmento de longitud b, M el punto medio de AB y D un punto arbitrario entre A y B, entonces la proposición se puede escribir en la forma:
AD·DB + MD2 = MB2 (2)
Como MB = b/2, llamando a DB = x, entonces MD = (b/2) – x y (2) se transforma en:
(b – x)x + (b/2 – x)2 = (b/2)2
Y como queremos resolver (b – x)·x = c2 quedará:
c2 + (b/2 – x)2 = (b/2)2
Por lo tanto (b/2 – x)2 = (b/2)2 – c2 y haciendo la raíz cuadrada de ambos miembros:
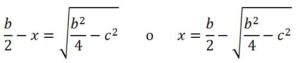
No obstante, la expresión algebraica de la Proposición 5 [c2 + (b/2 – x)2 = (b/2)2 ] nos permite apreciar el modo en que se usaba ésta para resolver este tipo de ecuación cuadrática mediante una construcción geométrica, ya que nos indica que la figura geométrica que debemos construir es un triángulo rectángulo de catetos, c y b/2 – x y de hipotenusa b/2.
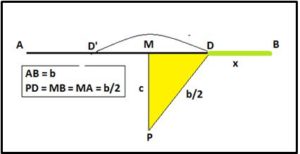
Para resolver geométricamente la ecuación
c2 + (b/2 – x)2 = (b/2)2
trazamos un segmento AB de longitud igual a b y sobre su punto medio M levantamos una perpendicular MP de longitud igual a c. Con centro en el punto P y radio b/2 trazamos una circunferencia que corta al segmento AB en los puntos D y D’: El segmento DB = AD = x es la solución de la ecuación propuesta. Es evidente que:
Si b/2 > c o, equivalentemente, b > 2c la ecuación tiene dos soluciones, porque la circunferencia de centro P y radio PD no corta a AB en dos puntos
Si b/2 < c o, equivalentemente, b < 2c la ecuación no tiene solución, porque la circunferencia de centro P y radio PD no corta a AB
Si b/2 = c o equivalentemente b = 2c la ecuación tiene una sola solución x = b/2
Podemos utilizar la Proposición 6 del Libro II de los Elementos para resolver la ecuación del tipo:
(b + x)·x = c2
Proposición 6: Si se divide el segmento AB en dos partes iguales y se añade, en línea recta otro segmento BC, el rectángulo comprendido entre la recta entera más la añadida y la recta añadida, más el cuadrado de la mitad del segmento AB es igual al cuadrado de lado la mitad de AB la recta más BC.
Podemos comprobar que llamando AB = b, BC = x, la Proposición 6 se puede expresar en la forma algebraica:
(b + x) x + (b/2)2 = (b/2 + x)2
Para resolver la ecuación cuadrática x2 + bx = c2 o (b + x)·x = c2 se procedía así:
(b + x) x + (b/2)2 = (b/2 + x)2 ⇒ c2 + (b/2)2 = (b/2 + x)2
Lo que nos lleva a la construcción de un triángulo rectángulo cuyos catetos son c y b/2 y la hipotenusa b/2 + x.
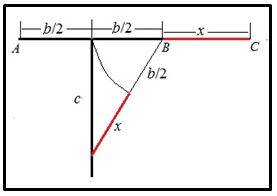
Procederemos como se indica en la figura: trazamos un segmento AB de longitud b y sobre su punto medio una perpendicular de longitud c. La hipotenusa medirá b/2 + x.
Si con centro en el punto B trazamos un arco de radio b/2 hasta cortar a la hipotenusa nos queda el segmento x que es una solución de la ecuación.
Es muy vistoso el ejemplo de la Aritmética de Al-Khwarizmi para resolver una ecuación cuadrática del tipo anterior con un cuadrado, realmente es un ejemplo didáctico para explicar el procedimiento que agiliza las cosas, la ecuación es:
(x+10)·x = 39 o x2 + 10 x = 39,
La operación de completar cuadrados que es lo que en esencia son las proposiciones del Álgebra Geométrica las aplica de forma rápida del siguiente modo:
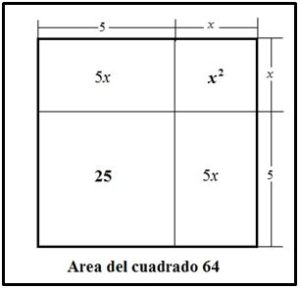
x2 + 10 x = 39 ⇒ x2 + 10 x + 25 = 39 + 25 ⇒
⇒ (x +5 )2 = 64 ⇒ x +5 = 8
Con lo que x = 3
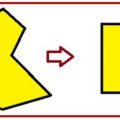
Para resolver la ecuación Al-Khwarizmi construyó un cuadrado de lado 8 y dentro de él un cuadrado de lado 5 la diferencia de sus lados nos dará la solución x = 3.
Realmente la resolución del problema resultaría menos llamativa si en lugar de 39 el término independiente fuera, por ejemplo, 17 y que el cuadrado mayor tuviera de lado √42.