El arte griego fue una búsqueda continua de la belleza ideal. La belleza para los griegos residía en la proporción y en la armonía. La representación artística del cuerpo humano o de los cuerpos de los animales tenía que ser bella, superando, en ocasiones, las “imperfecciones” de la naturaleza. Los objetos bellos debían guardar ciertas proporciones y las agrupaciones debían estar combinadas adecuadamente, esto es, de forma armoniosa. Esta belleza armónica tuvo su origen en la Escuela Pitagórica que afirmaba que todo el mundo real se podía reducir a números y a proporciones matemáticas. La proporción que representaba la belleza era la proporción áurea o número de oro.
Aristóteles (384-322 a. de C) en el capítulo V del libro I de la Metafísica (Metafísica, 985b, 986a) describe las creencias de los Pitagóricos:
… los llamados Pitagóricos fueron los primeros en cultivar las Matemáticas y no sólo hicieron avanzar a éstas, sino que nutridos de ellas, creyeron que sus principios eran los principios de todos los entes. Embebidos en este estudio, creyeron que los principios de las matemáticas eran los principios de todas las cosas. Y puesto que los números entre estos principios los primeros de todos y en ello les parecía contemplar muchas semejanzas con lo que es y lo que sucede, los Pitagóricos creían percibir en los números más que en el Fuego, en la Tierra y en el Agua, una multitud de analogías con lo que existe y lo que se produce. Tal combinación de números les parecía ser la Justicia, tal otra el Alma y el Entendimiento y tal otra el Tiempo oportuno; y lo mismo con todas las restantes; veían en los números las afecciones y las proporciones de las armonías. Como las demás cosas parecían asemejarse a los números y siendo por otra parte los números anteriores a todas las cosas, creyeron que los elementos de los números son los elementos de todos los seres, y que el cielo en su conjunto es una armonía y un número. Todas las correspondencias que veían en los números y en las armonías con las afecciones y con las partes de cielo. y con el orden universal, las reunían y reducían a un sistema. Y si en algún punto faltaba algo, se apresuraban a añadirlo para que toda su doctrina fuera coherente.
Platón (427-347 a. de C.)) en su Diálogo Timeo, escrito hacia el 360 a. de C, describió el mito de la formación del Cosmos a partir del Caos, con clara inspiración pitagórica. Demiurgo comenzó su obra a partir dos elementos, el Fuego y la Tierra, insertando entre ellos dos medias proporcionales: el Aire y el Agua, juntando así los cuatro elementos primordiales que formaban el Universo. Timeo de Locri expone claramente la idea de que los Cuatro Elementos estaban compuestos por entes matemáticos, tal como recoge Aristóteles en su Metafísica, con estas palabras:
“El fuego está formado por tetraedros; el aire, de octaedros; el agua, de icosaedros; la tierra de cubos; y como aún es posible una quinta forma, Dios ha utilizado ésta, el dodecaedro pentagonal, para que sirva de límite al mundo”.
Para los Pitagóricos la belleza en el mundo requería un orden y una forma, que estaba gobernados por relaciones numéricas. La proporción de la belleza era la proporción áurea, que aparece en las construcciones del antiguo Egipto y su importancia fue tan grade que sus propiedades geométricas fueron estudiadas en los Elementos de Euclides y está recogida en la Proposición 11 del libro 2, que dice:
Dividir una recta en dos partes, de manera que el rectángulo contenido por la recta (entera) y una de sus partes sea igual al cuadrado de la parte restante
Lo que quiere en lenguaje ordinario que un segmento rectilíneo está dividido según la proporción áurea cuando la relación entre la parte mayor y la parte menor es igual a la relación de todo el segmento con la parte mayor.
También se conoce la proporción áurea como dividir un segmento de longitud L en media y extrema razón. Expresado matemáticamente: Sea el segmento AB, y C un punto entre A y B talque AC > CB, entonces:
Esta proporción aparece en edificios como el Partenón o las Pirámides y puede observarse en la proporción de las esculturas, en la disposición de los objetos en los cuadros e incluso aparece en la actualidad en el diseño de diferentes objetos y logotipos. Los Pitagóricos matematizaron la belleza y descubrieron en el pentágono regular tres relaciones importantes que hicieron relacionar al pentágono y, más concretamente al pentágono estrellado, con la belleza:
Primera: Las dos diagonales que parten de un vértice del pentágono regular dividen al ángulo interior del pentágono, de 108º, en tres partes iguales (es decir las diagonales trisecan el ángulo). Los pitagóricos llamaron al pentágono estrellado, estrella de cinco puntas, Pentalfa o Pentagrama y lo tomaron como símbolo representativo o logotipo de su Escuela, por los secretos que guardaba.
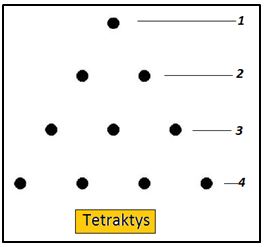
Segunda: (Es consecuencia de la anterior) En el hexágono se observan ángulos de 36º, 72º, 108º y 144º, que están en la relación 1, 2, 3, 4 de la tetraktys en la que se encerraba la armonía musical. ( Si una cuerda de longitud L daba una nota (Do), cuando vibraban L/2 emitía su octava (Do alto), si vibraban 3L/4 emitía su cuarta (Fa), si vibraban 2L/3 emitía su quinta (Sol).
Esta propiedad significaba para la Escuela Pitagórica que en el pentágono estaban escondidos los secretos de la armonía musical.
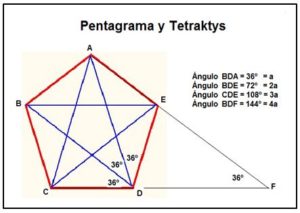
Tercera: Descubrieron que la diagonal y el lado del pentágono estaban relacionados por la razón áurea. Lo que significaba que el pentágono encerraba los secretos de la belleza visual.
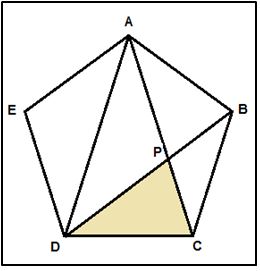
Consideremos el pentágono ABCDE. El triángulo ADC es semejante al triángulo DCP, porque tienen ángulos iguales 36º, 72º y 72º. Por lo tanto, ambos son isósceles, por lo tanto DP es igual al lado del pentágono, y también semejantes y verifican que:
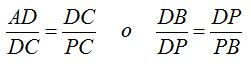
Donde DB es la diagonal del pentágono, DP es el lado del pentágono y PB es igual a la diagonal menos el lado. Y podemos escribir:
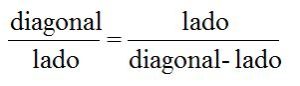Lo que significa que el lado y la diagonal están relacionados por la razón áurea. Si hacemos que el lado valga 1 y la diagonal mida x, quedará:
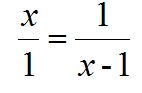Evidentemente, x es la razón entre la diagonal y el lado de un pentágono regular. Resolviendo esa ecuación, ya conocida, resultará que:
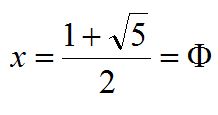Por lo tanto, la relación entre la diagonal y el lado de un pentágono regular es el número áureo.
El pentágono escondía los secretos matemáticos de la belleza musical y visual. Pero, además, descubrieron en él una sorpresa desagradable y era que el lado y la diagonal del pentágono eran magnitudes inconmensurables y que, por tanto, no podía haber una unidad común para expresar simultáneamente las medidas del lado y de la diagonal.
Esto significaba que no todas las relaciones entre magnitudes geométricas podían expresarse como relaciones entre números naturales. Era el descubrimiento de los números irracionales, que ponía de manifiesto que los objetos matemáticos no eran tan simples como se pensaba y superaban la idea aritmética de contar, lo que era irracional e impensable. La crisis de los irracionales hizo que los griegos desistieran de expresar las magnitudes geométricas en términos numéricos.
Pero, teniendo en cuenta que el pentágono estrellado era el símbolo de los pitagóricos, no resulta improbable que el primer par de segmentos inconmensurables fuera el lado y la diagonal del pentágono regular.
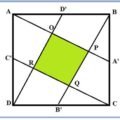
Partamos del polígono estrellado. Si queremos medir el lado y la diagonal con una unidad u, como el triángulo CDC’ es isósceles, entonces:
Lado = DC = DC’ y Diagonal = DC’ + C’B = Lado + C’B , C’B < Lado
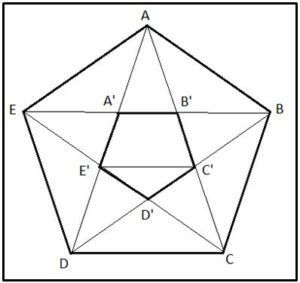
También deberemos poder medir con C’B con la misma u.
Consideremos el pentágono pequeño A’B’C’D’E (Denotaremos su lado y su diagonal con minúsculas)
lado = Diagonal – 2C’B
y como el triángulo CC’E’ es isósceles
diagonal = E’C’ = C’B.
Por lo tanto, debemos poder medir con la misma unidad a C’B con la misma unidad u, por tanto la
diagonal = C’B = E’C’ y lado = Diagonal – 2C’B
De dónde se sigue que el lado y la diagonal del pentágono pequeño se deben poder medir con la misma unidad, u.
Como se pueden seguir inscribiendo sucesivamente pentágonos estrellados y los pentágonos se hacen cada vez más pequeños llegamos a un pentágono cuyo lado sea menor que cualquier unidad que elijamos. Por tanto, el lado y la diagonal del pentágono son inconmensurables con cualquier unidad.
