Los números negativos no aparecieron de las necesidades humanas de contar y medir magnitudes físicas. El manejo de magnitudes negativas surgió en oriente, donde la aritmética fue la rama dominante de las matemáticas. La aparición se debió, seguramente, al hecho de que, mientras las medidas espaciales de un objeto se puede realizar con números positivos, en la aritmética, con la que se llevaban contabilidades, se podía tener dinero en caja o o tener deudas. El dinero se representaría con números positivos y las deudas con números negativos. Por esa razón los números negativos se llamaron en las primeras aritméticas números deudos. En el álgebra se les denominó números absurdos, seguramente porque aparecían al resolver ecuaciones que solucionaban problemas reales en los que interesaban las soluciones positivas y no se sabía explicar por qué la ecuación daba aquellas soluciones negativas, inesperadas y absurdas.
Los indios, además de aportar la numeración y el cero, fueron los primeros que distinguieron de forma simbólica los números positivos y los negativos. En la obra de Brahmagupta (598 – 668) apareció por primera de forma sistemática el cálculo con números negativos con el cero y manejaron las reglas numéricas de las operaciones, esto es, la regla de los signos.
Los números negativos se utilizaban en las aritméticas para comerciantes, que se usaban en las Escuelas de Abaco y se visualizaron al representarlos en la recta numérica y cuando se utilizaron en la Geometría Analítica fueron bien aceptados.
Las operaciones con números negativos se manejaban de forma perfecta y eficiente, justificadas, sin duda, porque se utilizaban en aritmética y en álgebra manejando una regla de los signos, que proporcionaba resultados coincidían que coincidían con lo que se esperaba en la realidad.
En los libros de texto se han dado diferentes a lo largo de la historia diferentes justificaciones de la regla de los signos, encaminadas a que los estudiantes aceptaran con naturalidad su uso, es decir, como si la regla de los signos fuera una consecuencia de lo ya sabido, pero en realidad los negativos eran unos números que ampliaban el conjunto de los números positivos y admitiendo esa regla se conservaba la concordancia con las reglas de cálculo establecidas para los números posotivos.
Si identificamos los números negativos como deudas no es difícil admitir que triplicar una deuda de cinco (-5) es como tener una deuda de quince (-15), lo que se traduce en que el producto de número positivo por otro negativo debe ser negativo: (+3)·(-5)=(-5)·(3) =-15
Admitido esto casi todos los autores de libros de Aritmética, desde el siglo XVI, han tratado de justificar la parte más delicada y nueva de esta parte de la Aritmética. El producto de dos números negativos ¿Cuál es el resultado de (-5)·(-7)?
(En lo que sigue, por facilitar la esctitura escribiré, por ejemplo, 5 el lugar de (+5))
El matemático holandés S. Stevin (1548-1620) justificaba la regla del producto de dos números negativos comprobando que su producto era el resultado que necesariamente tenía que dar para que se siguiera cumpliendo la propiedad distributiva del producto respecto de la suma,que cumplían los números naturales. Stevin justificaba la regla de los signos sencillamente porque hacía que salieran las operaciones. Para probarlo calculaba el producto (8-5)·(9-7) de dos formas:
En primer lugar: (8-5)·(9-7) = 3·2 = 6
En segundo lugar, aplicando la propiedad distributiva del producto de dos binomios, calculaba los sumandos
8·9 = 72
8·(-7)= – 56 (óctuplo de una deuda de 7)
(-5)·9= – 45 (nueve veces deuda de 5)
Quedaba la duda de cuál sería el valor de: (-5)·(-7) que debía + 35 o -35, pero para que el producto (8-5)·(9-7) sea de 6 es necesario que el producto (-5)·(-7) = +35, ya que
(8-5)·(9-7) = (+8)·(+9) + (+8)·(-7) + (-5)·(+9) + (-5)·(-7) = 72 – 56 – 45 + 35 = 6
El matemático suizo L. Euler (1707-1783) justificaba en sus Elementos de Álgebra (1770) los productos de número positivo por negativo de manera habitual y concluía que más por menos = menos y que menos por más = menos. Luego analizaba el caso menos por menos, por ejemplo, (-a) por (-b) y dice que el producto será ab; pero que era dudoso si debía llevar el producto el signo «+», o el signo «-» y se decidió que debía ser “-“ porque (-a) por (+b) da -(ab), y (-a) por (-b) no puede dar el mismo resultado que (-a) por (+b); y debe producir el signo contrario, esto es, +(ab); Por tanto, la regla menos por menos =más.
El matemático francés P.S. Laplace (1849-1827) en sus Lecciones de L’École normale (1795) justifica la regla de los signos y llegado al punto mayor dificultad (-a) por (-b) dice que el resultado del producto es el mismo que el de a por b. Para justificarlo observó que el producto de -a por +b, es – ab, ya que el producto no es más que (-a) repetido tantas veces como unidades hay en b y Como (-a)·(+b – b) = 0 aplicando la propiedad distributiva (–a)·(+b)+(-a)·(-b) = 0, de donde se deduce que el producto (-a)·(+b) y el producto (-a)·(-b), deben ser de signo contrario y como (–a)·(+b) =-ab entonces (-a)·(-b) debe ser igual a +ab y por lo tanto: menos por menos = más
F. Klein, en su obra Matemática elemental desde un punto de vista superior (1908) elabora una justificación de la regla de los signos en la forma geométrica siguiente:
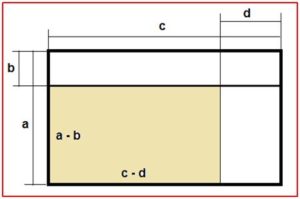
Sean cuatro números positivos a, b, c, y d, tales que a > b y c > d; por lo tanto, los números (a-b) y (c-d) serán positivos. Calculemos el producto (a-b) (c-d).
Para ello dibujemos un rectángulo de lados (a-b) y (c-d), cuya área será el producto buscado.
Este rectángulo es parte del rectángulo de lados a y c, tal y como se observa en la figura.
Para obtener (a-b)·(c-d) partiendo del área a·c, quitaremos el rectángulo superior de área b·c; después el rectángulo de la derecha de área a·d. Estos dos rectángulos contienen un rectángulo, que es intersección de ambos, de área b·d, que, lo hemos restado dos veces, por lo que habrá que añadirlo una vez una para obtener el área (a-b)·(c-d).
Con lo cual queda probado que (a-b)(c-d) = ac – ad – bc + bd y justificada la regla de los signos, ya que aplicando la distributiva (-b)·(-d) =+(bd)
Rey Pastor (1888-1962) y P. Puig Adam (1900-1960) en su libro Nociones de álgebra y trigonometría.(1946) justificaban de la regla de los signos con la información que proporcionaba un observador situado en el cero de una regla graduada que controlaba el desplazamiento de los móviles que pasan por delante de él . El observador asignaba orientación al espacio y al tiempo:
Los objetos que se desplazan a la izquierda se considera que llevan desplazamiento negativo y los que se mueven hacia la derecha los considera desplazamientos positivos.
En lo que se refiere al tiempo, el tiempo futuro (posterior a la observación) será positivo y el tiempo pasado tendrá valor negativo.
Para ilustrar la justificación supongamos un observador en Zaragoza que observa el tráfico ferroviario entre Barcelona y Madrid. En Zaragoza circulan trenes en los dos sentidos; los que van de Madrid a Barcelona que se tomarán como desplazamientos de signo positivo y los que van de Barcelona a Madrid que tendrán desplazamientos de signo negativo
El observador en Zaragoza toma como un origen de tiempos un momento dado, y considera como positivos los tiempos transcurridos desde ese instante y tiempos negativos los pasados.
Supongamos un tren que se desplaza a 100 Km/h hacia Barcelona (velocidad +100).
a) Después de dos horas (+2) de su paso estará (+100)·(+2) = +200 km. hacia Barcelona es decir +200. La operación se expresa abreviadamente (+100)·(+2) = +200
b) Dos horas antes (-2) el mismo tren, que lleva velocidad (+100) por ir hacia Barcelona, se encontraría estaría también a 200 km. del lado de Madrid, es decir, -200, y pondremos análogamente: (+100)⋅(-2) = -200
Si, por el contrario, el tren va hacia Madrid a 100 Km/h (velocidad -100) los signos se invierten,
y escribiríamos:
c) Después de dos horas (+2) de su paso estará (-100)·(+2) = -200 km. hacia Madrid es decir -200. La operación se expresa abreviadamente (-100)·(+2) = -200
d) Dos horas antes (-2) el mismo tren, que lleva velocidad (-100) por ir hacia Madrid se encontraría también a 200 km. del lado Barcelona, es decir, +200, y pondremos: (-100)⋅(-2) = +200
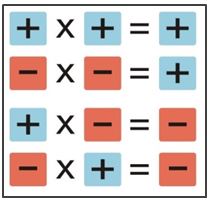
Hoy día parece natural en la enseñanza enunciar la regla de los signos sin justificación alguna. Simplemente se dice que para multiplicar dos números se multiplican los valores absolutos y el producto tendrá signo positivo si son iguales los signos de los factores y tendrá signo negativo si los factores tienen signos diferentes.
Los ejemplos anteriores demuestra que muchos grandes matemáticoa han intentado realizar una justificación de la regla de los signos, para presentar de una forma heurística y plausible la regla de los signos. Y, aunque los argumentos aportados no son una prueba, proporcionan una orientación más intuitiva de la regla , contribuye a hacerla plausible y nos acerca al pensamiento de los matemáticos, que en otros tiempos no la consideraron tan inmediata.