Leonardo de Pisa (1170 – 1240), conocido como Fibonacci, fue uno de los matemáticos medievales más influyentes. En 1202 escribió el libro de aritmética Liber Abaci en el que recogían las reglas del manejo de las operaciones con las cifras arábigas y sus aplicaciones para artesanos y comerciantes, así como una amplísima colección de problemas y ejercicios que serían referencia permanente en la matemática comercial hasta el siglo XV. El libro se ha traducido en muchas ediciones como El libro del ábaco que evoca el manejo de ese instrumento de cálculo, aunque es un libro dedicado al cálculo aritmético con cifras arábigas
Pero su nombre ha pasado a la historia unido a la sucesión infinita de números naturales conocida como sucesión de Fibonacci. La sucesión comienza con los números 1 y 1, se suma obteniendo 2 y luego los sucesivos términos se obtienen sumando los dos anteriores, resultando la sucesión: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
La sucesión apareció con la resolución de un problema sobre la cría de conejos que redactó así:
Una pareja de conejos adulta procrea una nueva pareja cada mes, se supone que los conejos alcanzan la madurez sexual a la edad de un mes, se aparean y el periodo de gestación es también de un mes, es decir, que una pareja de conejos recién nacidos tarda dos meses en procrear, a su vez, otra pareja.
Fibonacci planteó el problema partiendo inicialmente de una pareja de conejos jóvenes en un sistema aislado y suponiendo que no moría ninguno. Calculó cuántas parejas de conejos tendría al cabo de un año. La evolución de la población de conejos será la siguiente:
Inicio: Una pareja de conejos jóvenes (1 pareja)
Primer mes: Una pareja de conejos adultos. (1 pareja)
Segundo mes: Una pareja de conejos adultos y otra de conejos jóvenes (2 parejas)
Tercer mes: Dos parejas de conejos adultos y otra de conejos jóvenes (3 parejas)
Cuarto mes: Tres parejas de conejos adultos y dos de conejos jóvenes (5 parejas)
Quinto mes: Cinco parejas de conejos adultos y tres de conejos jóvenes. (8 parejas)
El último mes del año tendría 144 parejas de conejos. La sucesión será:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
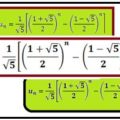
La sucesión de Fibonacci {fn} = {1, 1, 2, 3, 5, 8, 13 ,21, 34, 55, 89, … } se define por la ecuación recurrente fn + fn+1 = fn+2 , con los valores iniciales f1 = 1, f2 = 1
La sucesión de Fibonacci ha proporcionado muchas cuestiones curiosas relacionadas con sus propiedades aritméticas, por su relación con la belleza y con el número áureo. Las propiedades de la sucesión también han inspirado juegos y suscitado situaciones paradójicas. Como la paradoja de Hooper que describimos a continuación.
La paradoja fue expuesta por William Hooper (1742-1790) en sus Rational Recreations y la podemos expresar así: Es posible dividir un cuadrado en cuatro partes y, con ellas, construir un rectángulo que tenga (aparentemente) un área una unidad más o una unidad menos que el cuadrado.
La explicación de paradoja se encuentra en la siguiente propiedad de la sucesión de Fibonacci:
PROPIEDAD IMPORTANTE: Dados tres términos consecutivos cualesquiera de la sucesión de Fibonacci, el producto del primero por el tercero difiere del cuadrado del segundo en una unidad.
Más precisamente: Dados fn , fn+1 y fn+2 , entonces:
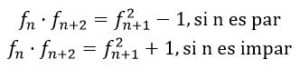
Como se puede comprobar en los siguientes ejemplos:
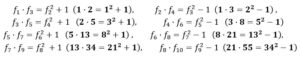
EJEMPLO1: (paradoja de Hooper): División de un cuadrado de lado 5 (área 25 u2) en cuatro partes y formar un rectángulo 3×8 (área 24 u2)
Para ello tomamos los términos de la sucesión de Fibonacci:
f4 = 3, f5 = 5 y f6 = 8, cumplen que : f4 · f6 = ( f5 )2 – 1, luego 3·8 = 52– 1

EJEMPLO2 (paradoja de Hooper): División de un cuadrado de lado 8 (área 64 u2) en cuatro partes y formar un rectángulo 5×13 (área 65u2)
Para ello tomamos los términos de la sucesión de Fibonacci:
f5 = 5, f6 = 8 y f7 = 13, cumplen que : f5 · f7 = ( f6 )2 + 1, luego 5· 13 = 82+1
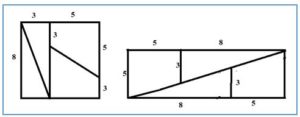
Explicación de la paradoja en el ejemplo 1: En la figura siguiente, los ángulos a y d son diferentes
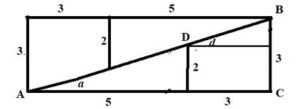
El tramo AD de la diagonal AB está más inclinado que el tramo DB, ya que el ángulo a tiene más pendiente (tg (a) = 2/5) que el ángulo d (tg (d) =1/3). El área del cuadrado unidad que se ha perdido al construir el rectángulo se ha “estirado” a lo largo de la diagonal AB
La explicación de la paradoja en el ejemplo 2 es análoga