
El astrónomo alemán J. Kepler (1571-1630) formuló sus tres famosas leyes sobre el movimiento de los planetas y sentó las bases de la astronomía moderna. Fue hijo de un mercenario del ejército del Duque de Alba y de una mujer que fue herborista y curandera y que fue acusada de brujería en varias ocasiones.
Kepler era un hombre profundamente religioso y pensaba que su deber cristiano era comprender el universo que Dios había creado, y estaba convencido de que los patrones que Dios había utilizado se basaban en las matemáticas y más específicamente en la Geometría.
Quizás por este sentimiento mágico y religioso de las matemáticas, Kepler estaba atento a descubrir relaciones numéricas entre las medidas tomadas en el mundo real que pusieran de manifiesto el pensamiento de Dios, encontrar relaciones que nos acercaran a conocer los planes del Creador.
Kepler, siguiendo la línea de pensamiento platónico, trató de conectar el mundo de las ideas puramente racionales con el mundo de la experiencia. Es decir, se dedicó a relacionar la Geometría con la realidad física. Imaginó un sistema planetario estructurado según la pauta racional de los cinco poliedros regulares, conocidos como sólidos platónicos.
En 1595, Kepler estaba convencido – según sus palabras – de haber comprendido los secretos del Creador y estableció un modelo del sistema planetario que utilizaba los sólidos platónicos para describir las distancias entre las órbitas de los planetas que se conocían entonces. En su modelo, Kepler partía de una esfera exterior, que representaba la órbita de Saturno dentro de la cual estaban inscritas sucesivamente: un cubo, la esfera de Júpiter, un tetraedro, la esfera de Marte, un dodecaedro, la esfera de la Tierra, un octaedro y finalmente la esfera de Mercurio.
Los resultados de sus especulaciones los publicó en su libro Mysterium Cosmographicum (1596), y en él, Kepler estableció dos resultados estrechamente relacionados: el primero mostrar la existencia de un patrón de organización del espacio que reflejaba la proporción entre las distancias planetarias respecto al Sol, es decir, los radios orbitales con un error menor del 10%. Además, en la obra conjeturó que distancias de los planetas al Sol estaban relacionadas con los periodos orbitales de cada planeta. Con su Sistema Planetario Kepler creía que había demostrado a priori, con la fuerza de la razón y el conocimiento la correcta ordenación de los cielos y, en suma haber demostrado la validez de Teoría Copernicana .
Pero en 1601, entró en contacto con los datos experimentales de las precisas observaciones del astrónomo danés Tycho Brahe (1546-1601) y estudió las relaciones numéricas entre ellas. Gracias a ellas pudo estudiar la órbita de Marte y demostrar que las órbitas de los planetas alrededor del Sol eran elípticas. Sus resultados los publicó en su Astronomía Nova (1609), donde calculó la órbita de Marte y publicó sus dos primeras leyes del movimiento planetario. En el año de 1619 Kepler publicó Harmonices mundi, Libri donde aparece su tercera la ley.
Leyes que tardaron casi veinte años de estudio en ser formuladas navegando en el mar de datos de Tycho

La visión platónica del mundo de Kepler lo llevó a descubrir relaciones numéricas curiosas que las consideraba como destellos luminosos del orden con el que Dios había creado el universo, pero, entre todas las relaciones numéricas, Keper destacaba dos: decía la Geometría tenía dos grandes tesoros: uno era el teorema de Pitágoras, que relacionaba los lados del triángulo rectángulo y el otro el número áureo, que daba las proporciones de la belleza. El primero podía compararse a una medida de oro, y el segundo a una piedra preciosa.
Kepler demostró una relación numérica que exponemos a continuación en forma de teorema.
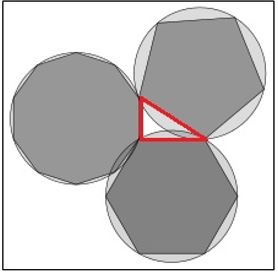
Teorema: En una circunferencia de radio R el lado del pentágono regular, el del hexágono regular y el del decágono regular inscritos en ella forman un triángulo rectángulo.
Demostración: La dividiremos en cuatro pasos:
Paso 1:
El lado del pentágono regular es mayor que el lado del hexágono y que el lado del decágono, por tanto, en caso de ser el triángulo rectángulo, será la hipotenusa.
Paso 2:
Lado del pentágono regular LP = 2R sen 36º , si R = 1 ⇒ LP = 2 sen 36º
Lado del decágono regular LD = 2R sen 18º, si R = 1 ⇒ LD = 2 sen 18º
Lado del hexágono regular LH = R, si R = 1 ⇒ LH = 1
hay que probar que (LP)2 = (LD)2 + (LH)2, es decir, que:
4 sen2 36º = 4 sen2 18º + 1
Paso 3:
El número de oro es 𝜙 = 2 cos 36º
Ya que, como 𝜙 es la relación entre la diagonal y el lado del pentágono regular, se tiene, razonando sobre el triángulo isósceles que forman la diagonal y dos lados del pentágono que:
𝜙= D/L y D = 2L cos 36º ⇒ 𝜙 = 2 cos 36º
Paso 4:
Haciendo en la relación trigonométrica: cos 2x = cos2 x – sen2 x x = 18º
cos 36º = cos2 18 – sen2 18 ⇔ cos 36º = 1 – 2 sen2 18 ⇔ 2 sen2 18 = 1 – cos 36º
Para probar que (LP)2 = (LD)2 + (LH)2, es decir, que transformaremos senos en cosenos:
4 sen2 36º = 4 sen2 18º + 1
4 (1 – cos2 36º) = 2 (1 – cos 36º ) +1
4 – 𝜙2 = 3 – 𝜙 ⇒ 𝜙2 = 1 + 𝜙
Como puede comprobarse, realizando el sencillo cálculo:
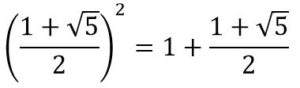
Teorema: El triángulo deKepler (y sus semejantes) es el único triángulo rectángulo que tiene sus lados en progresión geométrica.
Dem: Sean a, ar y ar2 cumplen:
a2 + (ar)2 = (ar2)2 ⇒ 1 + r2 = r4 ⇒ r4 – r2 -1 = 0 ⇒
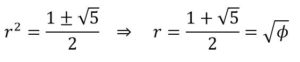
Que es la única solución real y positiva de la ecuación r4 – r2 -1 = 0 y, por tanto, el triángulo de Kepler tiene de medidas.
![]()




