Las teorías físicas son superadas o modificadas a medida que pasa el tiempo, sin embargo los resultados y los métodos de las matemáticas pueden caer es desuso, pero siempre mantienen su validez. La teoría del flogisto para explicar la combustión de los cuerpos fue desechada tras los estudios de química de A. Lavoisier (1743-1794) y del descubrimiento del oxígeno; las teorías que necesitaban postular la existencia del éter para explicar la propagación de la luz y las ondas electromagnéticas en el espacio vacío fue refutada como consecuencia del experimento de Michelson–Morley realizado en 1887; igualmente, la Hipótesis de la Tierra en expansión para explicar la formación de las cordilleras submarinas fue desbancada por la Deriva Continental de la A. Wegener (1880-1930) de 1912 y ambas fueron englobadas en la teoría de Tectónica de Placas nacida hace poco más de medio siglo.
Sin embargo, los métodos de las matemáticas mantienen su validez y los resultados de sus métodos y teorías se pueden seguir utilizando para resolver problemas. Es más, las diferentes teoría matemáticas permiten ofrecer diferentes puntos de vista de un problema y contribuyen a enriquecer la visión de conjunto. Para poner de manifiesto estas consideraciones resolveremos un problema de geometría constructiva haciendo uso de diferentes teorías o métodos matemáticos.
El problema es el siguiente:
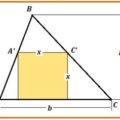
Determinar un triángulo equilátero que tenga un vértice sobre cada una de tres rectas paralelas dadas
MÉTODO 1.- (Geometría constructiva) Sean tres rectas paralelas a, b, c. Supondremos que la distancia entre a y b es p y que la distancia entre b y c es q.
Haremos el dibujo en tres pasos sucesivos:
Paso 1.- Dibujaremos un triángulo equilátero cualquiera DEF en cualquier posición y dividimos uno de sus lados, DF, por ejemplo, por un punto G, tal que:
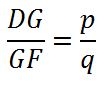

Unimos el punto G con el vértice E. Y por otros dos vértices del triángulo equilátero D y F trazamos paralelas a la recta GE.
Paso 2.- Como la figura que hemos dibujado es semejante a la que tratamos de determinar. A continuación haremos corresponder la recta EG con la recta b dada y, en esta situación, la recta EG (que coincide con la recta b) forma con el lado ED un ángulo α. Ahora tendremos el triángulo equilátero DEF en la posición que se observa en la figura siguiente:
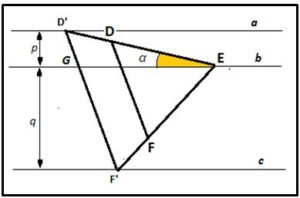
Paso 3. A continuación prolongamos el lado ED hasta cortar a la recta a en D’ y el lado EF hasta cortar a la recta c en F’. El triángulo equilátero ED’F’ es el triángulo buscado.
MÉTODO 2.- (Utilizando números complejos) Tendremos en cuenta que si se multiplica un número complejo z por (cos 60º + i sen 60º) el afijo de z gira un ángulo de 60º en sentido contrario a las agujas del reloj

Haremos coincidir una de las tres rectas con el eje de abscisas OX y sean las otras dos serán y = a e y = b.
Suponemos que uno de los tres vértices del triángulo equilátero es el origen de coordenadas
Los tres vértices serán del triángulo equilátero serán:
B(x1, b), A(x2, a) y C(0,0). Si los consideramos como afijos de números complejos, se tiene que:
(x1 + bi) = (cos 60º + i sen 60º)· (x2 + ai) ⇒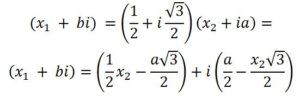
Por tanto, igualando las partes reales y las imaginarias

De donde:
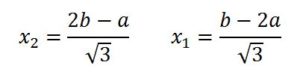
MÉTODO 3.- (Geometría Analítica) Partiendo de que las longitudes de los tres lados del triángulo son iguales. Si B(x1, b), A(x2, a) y C(0,0) son los vértices del triángulo equilátero planteamos las relaciones
d(C,B) = d(C,A) d(C,B) = d(A,B)
Que nos lleva a las ecuaciones:
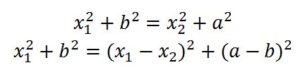
Resolviéndolas llegamos al mismo resultado que el obtenido por el método anterior.