Cuando hablamos de la Mecánica Newtoniana nos referimos a una de las mayores creaciones de la ciencia. En los Principia (1687), (Principios matemáticos de la filosofía Natural) de Newton aparecen definidos los conceptos matemáticos de una nueva ciencia y se asientan sus principios. En la obra se encuentran recogidos, y, en buena medida, resueltos, la mayor parte de los problemas mecánicos planteados hasta entones. Con Newton comenzó una mueva ciencia que sería el modelo de los paradigmas científicos.
Pero en el siglo que media entre la publicación de los Principia y la aparición de Mecánica Analítica (1768) de J.L. Lagrange (1736-1813), la Mecánica Newtoniana se transformó. Pasó de expresarse en el denso lenguaje de la geometría euclidiana a mostrar sus resultados en una ágil estructura analítica con la que se resolvían las cuestiones fundamentales de la Mecánica en términos de ecuaciones diferenciales. La Mecánica se expresó mediante el Cálculo Infinitesimal Leibniciano recogido, en primer lugar, en L’Analyse des Infiniment Petits pour l’Intelligence des Lignes Courbes (1696) del Marqués de L’Hôpital (1661-1704) y, en su forma más operativa y completa, por el Cálculo Infinitesimal, de L. Euler (1707-1783) recogido finalmente en Introductio in analysin infinitorum (1748)
El lenguaje geométrico utilizado por Newton en Principia y su planteamiento del Cálculo Infinitesimal, ya en forma geométrica con las Primeras y Últimas Razones o en forma dinámica, en términos de fluxiones y fluyentes, tuvo importantes consecuencias en la diferente evolución de las matemáticas y de la ciencia en Inglaterra y en resto de Europa. En esta separación tuvo gran influencia el prestigio y la devoción que sentía todo el mundo científico por la obra de Newton, el Cálculo de Fluxiones utilizado por los matemáticos ingleses de la primera mitad del siglo XVIII y, además la agria disputa desatada, a principios del siglo XVIII, sobre la prioridad del descubrimiento del Cálculo Infinitesimal entre los partidarios de Newton y Leibniz.
La situación dio como resultado que los matemáticos ingleses persistieran en el desarrollo del cálculo geométrico y fluxional, mientras que los matemáticos del resto de Europa siguieran el cálculo de Leibniz, recogido al principio fundamentalmente en el libro del L’Hôpital
La obra de Newton necesitaba revisiones, aclaraciones y ampliaciones. En la segunda edición de Principia, revisada por Roger Cotes (1682-1716) aparecía un Prefacio en el que apoyaba la superioridad científica de los principios de Newton sobre la entonces popular teoría de los vórtices cartesianos, porque contradecían la Ley de Gravitación confirmada experimentalmente
Los Principia necesitaban divulgación, porque no eran fáciles de entender. W. Gravesande (1688-1742) escribió el libro Elementos matemáticos de la Filosofía Natural, confirmada por Experimentos; o, una Introducción a Filosofía newtoniana (1720), publicado en Leiden, donde se mostraban experimentos para enseñar los fundamentos la Mecánica de Newton. El libro fue traducido del latín al inglés por Jean T. Desaguliers (1683-1744) miembro de la Royal Society de Londres, ayudante de Newton, que escribió otra obra en dos volúmenes, Curso de Filosofía Experimental (1734), para hacer asequible la Mecánica de Newton. También H. Pemberton (1694-1771), que había revisado la tercera edición de los Principia de 1726 escribió Visión de la Filosofía de Sir Isaac Newton (1728) y más tarde Elementos de filosofía newtoniana. No obstante, los grandes divulgadores en Europa de las teorías de Newton fueron Voltaire, pseudónimo de F. M. Arouet (1694–1778) con su obra Elementos de la filosofía de Newton (1738) y G. Émilie de Breteuil, Marquesa de Châtelet (1706-1749) con sus Instituciones de Física (1740)
Las matemáticas inglesas y continentales tomaron derroteros diferentes B. Taylor (1681-1735) en su obra más famosa, Methodus Incrementorum Directa et Inversa (1715), desarrolló una nueva rama de las matemáticas conocida como Cálculo de las Diferencias Finitas. Y Colin Maclaurin (1698-1746), en su obra monumental Treatise of Fluxions (1742), expuso una física adaptada a los Principia utilizando el método de fluxiones, aunque sustentado con una base axiomática. Fue el intento genial, pero que no pudo con empuje del Cálculo Infinitesimal, que se desarrollaba en el continente para lograr una síntesis de las diferentes corrientes de pensamiento matemático de Newton.
A mediados del siglo XVIII los matemáticos continentales, como Euler o Lagrange, estaban inspirados por la filosofía cartesiana y seguían el cálculo en la línea señalada por Leibniz y la dirección era muy diferente de la seguida por Maclaurin y los matemáticos ingleses.
Euler escribió textos sobre Cálculo, Mecánica y Álgebra que se convirtieron en modelos para otros autores interesados en estas disciplinas. De hecho Euler, en su obra Mecanica, o Ciencia del Movimiento, Expuesta en Forma analítica (1736) presentó la Dinámica de Newton, en forma de Análisis Matemático e inició en el camino había de marcar el siglo en el estudio de la materia. En Introductio in analysin infinitorum (1748) desarrolló el Análisis basado en el concepto de función definida por series infinitas y alcanzó la cima en este campo con Decouverte d’un nouveau principie de Mécanique (1750). Euler realizó el proceso de matematización de las leyes newtonianas, tarea que no es trivial, ya que realizó un doble proceso. Desde el punto de vista puramente matemático: cambió el lenguaje geométrico por el del Cálculo Infinitesimal que usaba ecuaciones diferenciales en la Mecánica y realizó la primera de la fundamentación y axiomática de la Mecánica Racional.
El éxito de Euler fue tan grande que sirvió de modelo a los matemáticos durante mucho tiempo. J. Bernoulli (1667-1748) se lo reconoce en una carta que le dirigió diciendo: “Yo represento al análisis superior en su infancia, pero tú lo estás llevando a su estado adulto” y P.S. Laplace (1749-1827) decía: “Leed a Euler, leed a Euler, él es el maestro de todos nosotros”.
Además, desde el punto de vista filosófico, Euler aportó la convicción Cartesiano-Leibniciana de que en Física no existían fuerzas que actuaran a distancia y la Física de Newton se enriqueció con la tradición leibniziana con aportaciones como: la Teoría del Potencial, la relación la energía con la integral del momento lineal, además de sentar las bases de la Teoría de Fluidos desde una perspectiva de energetista muy diferente al estudio de fluidos que realizó Newton en la sección IX del libro II de los Principia.

En la Mécanique (1750), Euler enuncia la segunda ley de Newton con notación cartesiana y en términos del Cálculo Diferencial de Leibniz del siguiente modo:
El movimiento de una masa puntual, M, motivado por una fuerza F. Si la distancia de M al plano es x, se descomponen todas las fuerzas que actúan sobre M en un instante dado en direcciones paralelas y perpendiculares al plano. Un instante de tiempo, después, dt, la distancia de M al plano será x+dx, se cumple que 2Mddx= ∓dt2 , esta es para Euler la fórmula fundamental.
Para determinar el movimiento en el espacio de una masa puntual M hay que referirlo a tres planos. Llamando x, y y z a las distancias a cada uno de ellos (ccordenadas espaciales) y descomponiendo la fuerza F que actúa sobre la partícula a lo largo de las direcciones perpendiculares a los tres planos, y siendo esas fuerza Fx, Fy y Fz el movimiento de la particula estará contenido en las fórmulas (según notación de Leibniz):
2 M ddx = ∓ Fx dt2 2M ddy = ∓ Fy dt2 2Mddz = ∓ Fz dt2
En notación actual la descomposición de fuerzas se expresa:
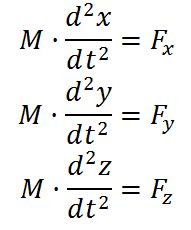
Que permitía expresar la segunda ley de Newton en el lenguaje del Cálculo Infinitesimal de Leibniz. El trabajo de Euler expresaba la Mecánica de Newton en términos de Cálculo, además, la enriquecía con nuevos conceptos y fue un paso decisivo en la Mecánica Racional y constituyó el hito fundamental del triunfo de la ciencia continental sobre la ciencia inglesa, que estaban claramente enfrentadas por diferentes motivos. En primer lugar la polémica, ya reseñada, sobre la prioridad de la invención del Cálculo Infinitesimal entre Newton y Leibniz.
Otro motivo de rivalidad ente ambas ciencias fue la polémica suscitada por la forma de la Tierra que enfrentó a la Mecánica Racional expuesta por Newton en sus Principia con la astronomía práctica que venían realizando los astrónomos profesionales. Newton en los Principia dedujo que la Tierra no era una esfera perfecta, como se creía hasta entonces, sino que estaba achatada por los polos. Por su parte, J. Cassini (1677-1796), astrónomo del Observatorio Astronómico y miembro de la Real Academia de Ciencias, había estimado, con medidas tomadas sobre la superficie terrestre y publicadas en su libro De la grandeur et de la figure de la Terre (1720), que la forma de la Tierra debía ser alargada hacia los polos y no achatada, como afirmaba Newton.
Esta diferencia de resultados desató una intensa polémica que enfrentó la Astronomía Práctica de los Cassini con la Mecánica Racional de Newton, a la Royal Society con la Academie Française y, finalmente, a la Ciencia Inglesa y con Ciencia Francesa. La Tierra no era una esfera perfecta, pero ¿estaba achatada por el ecuador o por los polos?
En el año 1735, el rey francés Luis XV decidió disipar las dudas midiendo la longitud de un minuto de meridiano en las proximidades del Polo Norte y en el Ecuador, para lo que organizó dos expediciones. Una a laponia dirigida por el astrónomo y matemático P.L.M. Maupertuis (1698-1759) y otra, dirigida por L. Godin (1704-1760) a Quito. Las medidas de los expedicionarios comprobaron que los grados de meridiano medidos en el Ecuador eran mayores que los medidos en Laponia, por lo que las medidas dieron la razón a las tesis de Newton, la Tierra estaba achatada por los polos.
La Mecánica Newton triunfó sobre la Astronomía Práctica que defendía la ciencia continental, pero el Cálculo Infinitesimal de Leibniz tenía una notación muy superior al de Newton. En esta situación Euler, superando dificultades matemáticas, físicas, filosóficas y de orden político, supo tomar los problemas de Newton y aplicarles el Cálculo Leibniciano, mejorando de forma genial la Mecánica recogida en los Principia, Euler no fue un simple traductor-adaptador de la obra de Newton
Euler realizó profundas reflexiones filosóficas sobre la imagen del mundo que proporcionaba la física de los Principia porque apreciaba ciertas incongruencias entre el principio de inercia y la fuerza de atracción universal. En Cartas a una princesa de Alemania sobre diversos temas de física y filosofía (1768), que es seguramente uno de los primeros libros de divulgación científica general, expone sus dudas sobre las fuerzas y su origen. Se sorprendía de cómo era posible que la fuerza de inercia, que era una facultad por la que un cuerpo permanecía en el mismo estado y por la que se oponía a cualquier cambio, a no ser que hubiera una fuerza externa que lo modificara, podía compartir espacio con las fuerzas de atracción que lo hacían cambiar de estado. Dudaba de que dentro de un cuerpo hubiera fuerzas de inercia que los hacían permanecer en un estado y otras fuerzas que tendieran a hacerle cambiar de estado, Euler atribuyó el origen de las fuerzas a una facultad de los cuerpos que era la impenetrabilidad. Así lo recoge en la carta 79 de Cartas a una princesa de Alemania:
“La misma facultad de los cuerpos por medio de la que procuran permanecer en el mismo estado, es capaz de proporcionar fuerzas que cambien el estado de otros”
Y sigue en la carta 79

… sin embargo recibe un rudo golpe la atracción como cualidad intrínseca de los cuerpos….los cuerpos no actúan sobre otro sino para mantener su impenetrabilidad
La labor de Euler fue recogida y ampliada por J. L. Lagrange (1736-1813), que introdujo un cambio en los axiomas estudió un sistema de partículas cuando las fuerzas que interactuaban entre si procedían de una función potencial. Probó que su expresión del Principio de Mínima Acción junto con la Ley de la Conservación de la Energía, eran equivalentes a las Leyes de Newton del movimiento, y podía emplearse como una formulación alternativa muy poderosa para resolver los problemas de la Mecánica Clásica.