Los orígenes del problema conocido como problema de Delos o de la duplicación del cubo se remontan a la leyenda. Se cuenta Pericles murió en el año 427 a.C. como consecuencia de una epidemia de peste que acabó con la cuarta parte de la población ateniense. Para acabar con la peste Atenas envió una comisión de notables a consultar al oráculo de Apolo en Delos, para preguntarle cómo se podría acabar con la epidemia, a lo que el oráculo contestó que era necesario duplicar el altar cúbico dedicado a Apolo. Para cumplir con la respuesta del oráculo los atenienses dedicaron a Apolo un altar de lado doble que el anterior, pero la peste siguió ya que no se había se había cumplido al indicación del oráculo, puesto que no habían duplicado el altar, sino que lo habían hecho ocho veces mayor.
El problema trataron de resolverlo según las exigencias metodológicas de la Matemática Griega que imponía el uso exclusivo de la regla y el compás. Pero el problema de la duplicación del cubo mediante el uso de la regla y el compás no tiene solución, ya que con regla y compas se pueden resolver problemas que se puedan reducir a rectas y circunferencias, es decir, a ecuaciones de primer y segundo grado. Calcular el lado de un cubo cuyo volumen sea el doble del otro cubo de volumen unidad es equivalente a calcular el lado x de un cubo tal que x3 = 2, es decir, es lo mismo que resolver la ecuación x3 – 2 = 0. Por lo tanto, es preciso que alguna de las raíces de esa ecuación se pueda construir con regla y compás.
En teoría de ecuaciones algebraicas hay un resultado que dice que si una ecuación de tercer grado con coeficientes racional no tiene ninguna raíz racional, entonces ninguna de sus raíces es construible sobre Q, como la ecuación x3 – 2 = 0 no tiene ninguna raíz racional, entonces no tiene raíces construibles.
No obstante los problemas difíciles o sin solución han estimulado a lo largo de la historia la mente de grandes científicos. Eratóstenes de Cirene (284-192 a. J.C.) resolvió) el problema de la duplicación del cubo (aunque no con regla y compás) inspirándose la duplicación del cuadrado.
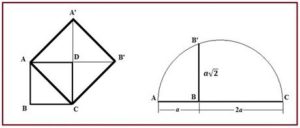
Duplicar un cuadrado de lado a es construir un cuadrado de área doble y el lado de ese cuadrado será media proporcional entre a y 2a. Es decir, el lado del cuadrado será una longitud x tal que:
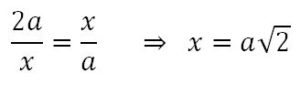
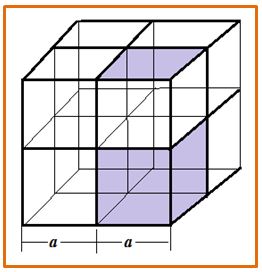
Eratóstenes, en su obra La duplicación del cubo, contó la historia que dio lugar al problema diciendo que cierto autor trágico, seguramente Eurípides (480-406 a. de J.C.), hizo aparecer en escena al rey de Creta Minos en el momento que se construía la tumba con forma de cubo de su hijo Glauco, y al comprobar que sólo medía cien pies por cada lado dijo: es un espacio muy pequeño para sepulcro de un rey. Duplicadla conservando su forma cúbica duplicando cada lado. Es evidente que Minos se equivocaba, porque duplicando los lados de una figura plana se cuadruplica, mientras que una sólida se octuplica, tal como se puede observar en la figura siguiente:
Hipócrates de Quios (470-410 a de J.C.) sabía que para calcular el lado de un cuadrado cuya superficie fuera igual a la de un rectángulo de lados a y b se insertaba una media proporcional entre a y b, de modo que el lado del cuadrado era x verificaba que x =√ab. Hipócrates determinaba x del siguiente modo geométrico que se muestra, que es un método gráfico de determinar la media geométrica. Para determinar un cuadrado de área doble que otro de lado a basta con insertar una media proporcional entre a y 2a, y se obtiene un lado x = a √2, tal y como se indica en la construcción siguiente
Los geómetras extendieron el procedimiento empleado para la duplicación del cuadrado a la duplicación del cubo. Hipócrates descubrió que el problema de calcular el lado un cubo de volumen doble que otro cubo dado de lado a era equivalente al de determinar dos medias proporcionales entre 2a y a. Esto es, equivalía a hallar dos valores x e y que cumplieran la relación:
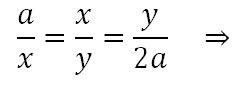
⇒ ay = x2 y y2= 2ax, eliminando el medio proporcional y de ambas ecuaciones se obtiene que 2a3 = x3, es decir, que:
![]()
Y el cubo de lado x tiene doble volumen que el cubo de lado a.
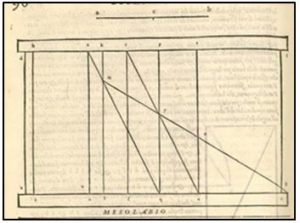
El problema de construir dos medias proporcionales no se puede hacer con regla y compás, pero los científicos griegos diseñaron algunos artilugios mecánicos que permitían resolver el problema dejando aparte las potentes restricciones que imponían el solo uso de la regla y el compás. Eratóstenes de Cirene (284-192 a.J.C.) construyó un aparato mecánico, llamado mesolabio que permitía insertar un número cualquiera de medias proporcionales entre dos magnitudes dadas. Él lo decía con estas palabras:
“…he inventado un sencillo procedimiento mecánico que no sólo permite encontrar dos medias proporcionales, sino tantas como se quiera y es muy útil para todos los que deseen duplicar o ampliar altares, casa, medidas de capacidad, catapultas y otros objetos análogos”
A continuación se describe el mesolabio de Eratóstenes que consta de tres triángulos rectángulos BFE, CHG y DJI que se pueden desplazar horizontalmente sobre las guías paralelas ABCD y EFGHIJ. El rectángulo BFE se deja fijo en el extremo de las guías y los otros dos se desplazan.
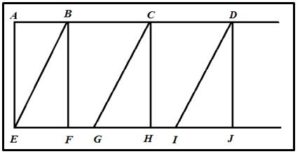
En el desplazamiento la hipotenusa de cada uno de los dos triángulos móviles cortará a los cateto del colocado a su izquierda en dos puntos que designaremos con las letras P y la hipotenusa del otro cortará al segundo en punto N . Si se desea insertar dos medias proporcionales entre a y 2a se procederá del modo siguiente:
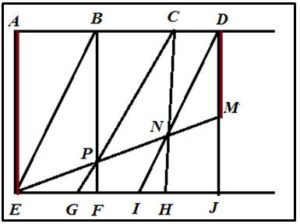
Se toma AE = 2a sobre el travesaño perpendicular que une las dos guías.
Tomaremos a = DM sobre el triángulo DJI.
Se desplazan los triángulos Se desplazan los triángulos CHG y DJI hasta que los puntos E, P, N y M estén alineados.
Los triángulos EBP, PCN y NDM con semejantes y cumplen que:
![]()
los segmentos CN y BP serán las dos medias proporcionales que se deseaban insertar.
![]()
la x es el lado del cubo.


