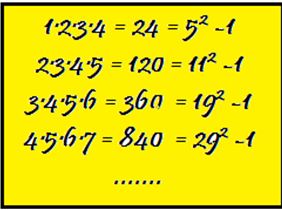
El producto de enteros consecutivos tienen propiedades interesantes y aquí presentamos algunas en forma de ejercicios.
EJERCICIO 1.- Probar que el producto de cuatro enteros consecutivos es divisible entre 24.
Solución 1: Teniendo en cuenta que el número de subconjuntos posibles de cuatro elementos que se pueden formar con n elementos es, evidentemente, un número entero y que viene dado por:
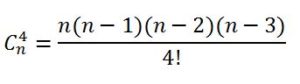
Entonces n(n-1)(n-2)(n-3) es divisible por 4! = 4·3·2 = 24
Solución 2: Veremos que el producto de cuatro enteros consecutivos es divisible por 8 y por 3.
- En el producto de cuatro números consecutivos:
P = n (n+1)(n+2) (n+3)
hay siempre dos factores pares (y, además, uno o dos factores que son múltiplos de tres)
Como hay dos factores pares uno será de la forma 2p y otro de la forma 2p +2, con p entero, y el producto:
2p (2p +2) = 4 p (p+1) = Múltiplo de ocho,
Ya que p (p+1) es múltiplo de dos. Por lo tanto P es múltiplo de ocho.
- El resto de la división de un número entero entre tres puede dar 0, 1, o 2. Como en el producto P = n (n+1)(n+2) (n+3) hay cuatro factores consecutivos los darán los cuatro restos (y alguno se repetirá), por lo tanto
P = n (n+1)(n+2) (n+3) = Múltiplo de tres,
por lo tanto, P = n (n+1)(n+2) (n+3), que es múltiplo de tres y de ocho, es múltiplo de 24.
Este resultado es un caso particular del teorema más general siguiente:
Si n es un número entero mayor que la unidad, el producto de cualquier número n de enteros consecutivos es divisible entre n!
La demostración se realiza por inducción sobre n, en el producto de n enteros comenzando por a, llamando 𝜋a el producto de n enteros consecutivos, siendo a el menor de ellos y 𝜋a = a(a+1)(a+2) ····(a+n-1)
EJERCICIO 2.- El producto de cuatro enteros consecutivos es igual a N = 7590024. ¿Cuáles son dichos números?
Solución : Los números serán a1 = a -1, a2 = a, a3 = a +1 y a4 = a +2
Sabemos que N = a1 ·a2 · a3 · a4 = (a -1)· a·(a+1)·(a+2) = 7.590.024.
Como N = 7590024 no acaba ni en cero ni en cinco, ninguno de los cuatro factores consecutivos acabará en ni en cero Luego tienen que acabar en 1, 2, 3 y 4 respectivamente o en 6, 7, 8, 9
También sabemos que la media geométrica es menor que la necia aritmética
La media geométrica es mayo que el menos de los números, por lo tanto:
![]()
Pero como la media geométrica es menor que la aritmética y la media aritmética de
(a -1), a, ( a+1), (a+2) es a+ 0,5, se tiene que:
a < 52,49 < a+0,5, luego 0 < 52,49 – a < 0,5
Por lo tanto, a = 52 y a1 =51, a2 = 52, a3 = 53, a4= 54 .
Solución: 2 (Realizando los cálculos con el programa Derive):
Sabemos que (a-1)a(a+1)(a+2) = 7590024 entonces a4 + 2a3 – a2 – 2a – 7590024 = 0, factorizando: (a– 52)(a + 53)(a² + a + 2754) = 0. Como a² + a + 2754 = 0 tiene raíces imaginarias y a + 53 = 0 tiene la raíz negativa a = – 53, solo puede ser a = 52 y así los factores son 51, 52, 53 y 54
EJERCICIO 3. – Determina cuatro números naturales consecutivos cuyo producto sea 3024.
Solución: Como 3.024 no acaba ni en 0 ni en 5, ninguno de los cuatro números será divisible por 5. Es decir, no acabará ni en cero ni en cinco.
Si los números fueran mayores que 10, el producto sería mayor que 10.000. Luego solamente tenemos como posibles soluciones las cuaternas de números 1, 2, 3, 4 y 6,7, 8, 9. Evidentemente, los números buscados son 6, 7, 8 y 9. Como se puede comprobar 3024 = 6·7·8·9
Ejercicio 4.- El producto de cuatro números naturales consecutivos verifica lo siguiente:
1·2·3·4 = 24 = 52 -1
2·3·4·5 = 120 = 112 -1
3·4·5·6 = 360 = 192 -1
….
¿Se verifica siempre?
Solución: En una Hoja de Cálculo se puede comprobar:
| n | n+1 | n+2 | n+3 | Producto | Producto +1 | Raiz |
| 2 | 3 | 4 | 5 | 120 | 121 | 11 |
| 3 | 4 | 5 | 6 | 360 | 361 | 19 |
| 4 | 5 | 6 | 7 | 840 | 841 | 29 |
| 5 | 6 | 7 | 8 | 1680 | 1681 | 41 |
| 6 | 7 | 8 | 9 | 3024 | 3025 | 55 |
| 7 | 8 | 9 | 10 | 5040 | 5041 | 71 |
| 8 | 9 | 10 | 11 | 7920 | 7921 | 89 |
| 9 | 10 | 11 | 12 | 11880 | 11881 | 109 |
| 10 | 11 | 12 | 13 | 17160 | 17161 | 131 |
| 11 | 12 | 13 | 14 | 24024 | 24025 | 155 |
| 12 | 13 | 14 | 15 | 32760 | 32761 | 181 |
| 13 | 14 | 15 | 16 | 43680 | 43681 | 209 |
| 14 | 15 | 16 | 17 | 57120 | 57121 | 239 |
| 15 | 16 | 17 | 18 | 73440 | 73441 | 271 |
| 16 | 17 | 18 | 19 | 93024 | 93025 | 305 |
| 17 | 18 | 19 | 20 | 116280 | 116281 | 341 |
| 18 | 19 | 20 | 21 | 143640 | 143641 | 379 |
| 19 | 20 | 21 | 22 | 175560 | 175561 | 419 |
| 20 | 21 | 22 | 23 | 212520 | 212521 | 461 |
Las siguientes identidades nos demuestra que la propiedad se verifica para todo n:
n·(n + 1)·(n + 2)·(n + 3) + 1 = n4 + 6·n3 + 11·n2 + 6·n + 1 = (n2 + 3·n + 1)2
Utilizando el método de los coeficientes indeterminados:
n4 + 6·n3 + 11·n2 + 6·n + 1 = (n2 + a·n + b)2
desorrollando e igualando coeficientes resulta el sisema de sistema de ecuaciones sobredeterminado:
2a = 6 a2 + 2b = 11 2ab = 6 y b2 = 1
del que trivialmentese obtienen las soluciones a = 3 y b= 1




