Los criterios de divisibilidad se aprenden en la aritmética elemental y sirven para reconocer cuando un número es múltiplo, o es divisible. Se estudian los criterios de divisibilidad por dos, por tres, por cuatro, por cinco, por ocho, por nueve por once. Aunque la obtención de los diferentes criterios de divisibilidad tiene un método común de obtención, algunos son complicados y difíciles de recordar, ¿Cuáles son los criterios de divisibilidad por siete, por trece o por 17?
Trabajar con los criterios nos hace profundizar en los conceptos de múltiplos, divisores, divisibilidad, congruencias, etc. Pero en un tiempo, en el que pocos hacen matemáticas con sólo lápiz y papel, en el mundo de los ordenadores, se puede utilizar su potencia de cálculo, para resolver cuestiones de números y de divisibilidad.
Ejercicio 1.- Determinar las cifras x e y para que el número 1x579y sea divisible entre 72.
Solución: 72 = 8 · 9, y utilizaremos los criterios de divisibilidad por 8 y por 9
Para que 1x579y sea divisible por 8, el número 78y tiene que ser múltiplo de 8 ⇒ y=2-
Para que 1x5792, sea divisible por 9, la suma de la cifras de 1x5792 tiene que ser múltiplo de 9 ⇒ 24 + x =27
⇒ x =3. Por tanto, el número buscado es 135792 que es divisible por 72 135792 = 72·1886
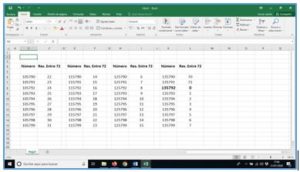
Este ejercicio se podría resolver con la Hoja de Cálculo Excel y con la función =RESIDUO(105790;72), que da el resto de 105790 entre 72 . Calculando dos restos entre 72, de 105790 a 105799 entre 72, de 115790 a 115799 entre 72,…. Hasta de 195790 a 195799 entre 72. La solución (o soluciones) serán los números que den resto cero.

Ejercicio 2.– Sabiendo que el número 13xy45z es divisible entre 792 determinar la cifras x, y, z.
Solución: Como 792 =23·32·11 = 8·9·11, tendrá que ser divisible por 8, por 9 y por 11:
Para que sea divisible por 8, las tres últimas cifras deben ser un múltiplo de 8. Por lo tanto el número, tiene que acabar en 456. Ya que 456 = 8·57. Luego z = 6.
Para que sea divisible entre 9, la suma de las cifras 13xy456 debe ser múltiplo de 9, es decir:
x + y +19 debe ser múltiplo de 9 ⇒ x + y +19 = 9n, que da lugar a las ecuaciones:
x + y +19 = 27 ⇒ x + y = 8 (1)
x + y +19 = 36 ⇒ x + y = 17 (2)
Para que sea 13xy456 sea múltiplo de 11 la suma de las cifras de lugar impar menos la suma de las cifras que ocupan lugar impar debe ser 0, 11 o múltiplo de 11, es decir:
1-3 + x – y + 4 – 5 + 6 = x – y + 3 = 11 n, que da lugar a las ecuaciones:
x – y + 3 = 0 ⇒ x – y = -3 (3)
x – y + 3 = 11 ⇒ x – y = 8 (4)
Para determinar x e y emplearemos los cuatro sistemas de ecuaciones:
- y (3) x + y = 8, x – y = -3 ⇒ x = 5/2, y =11/2 (No, los resultados no son cifras)
- y (4) x + y = 8, x – y = 8 ⇒ x = 8, y = 0 (válida 1380456)
- y (3) x + y = 17, x – y = -3 ⇒ x = 7, y =10 (No)
- y (4) x + y = 17, x – y = 8 ⇒ x = 25/2, y = 9/2 (No)
La única solución 1380456
Ejercicio 3: Obtener el criterio de divisibilidad por 7 en base diez. Calcula x para que 123×45 sea divisible por 7
Solución: Criterio de divisibilidad por 7

El número 123×45 será divisible por 7 si 5·1+ 4·3 + 2x – 1·3 – 2·3 – 2·1=7k ⇒ 17+ 2x -11 =7k ⇒
2x+6 = 0 x < 0 ⇒ no es cifra
2x+6 = 7 ⇒ x =1/2 ⇒ no es cifra
2x+6 = 14 ⇒ x =4 ⇒ 123445
2x+6 = 21 ⇒ x =15/2 ⇒ no es cifra
2x+6 = 28 ⇒ x =11 ⇒ no es cifra
Podríamos resolverlo con la Hoja de Cálculo con la función: =RESIDUO(123045;7), como se indica en la imagen siguiente:
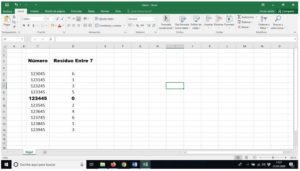
Ejercicio: Calcula con la Hoja de Cálculo x e y para que 18967xy sea divisible por 23 Sol: x = 4, y =1