Cuando se comparan entre sí dos cantidades, A y B y consideramos que la B es la unidad con la que deseamos medir la A, puede ocurrir que:
La A contenga exactamente a cierto número de las unidades B o de sus partes alícuotas. En tal caso, A se dice que se dice que es conmensurable, y el número que la representa la relación entre ambas es un número racional. Es lo que sucede cuando queremos expresar una magnitud A de medida 5 en función de otra magnitud B de medida 4. A no se puede expresar exactamente en unidades B ni en décimas de B, pero si puede hacerse en exactamente en centésimas de B y podemos decir que A mide por 125 centésimas de B. La relación 5/4 = 1,25 es un número racional (ya sea entero o fraccionario).
O que A no contenga exactamente a un número de las unidades B ni de sus partes alícuotas. En tal caso, A se dice que se dice que es inconmensurable, y el número que la representa la relación entre ambas es un número irracional. Es lo que sucede cuando queremos expresar una magnitud A de medida Ö2 en función de otra magnitud B de medida 1. A la medida de no se puede expresar exactamente en unidades B ni en décimas de B, ni en centésimas ni en ninguna otra división de B en partes iguales. Ö2 un número racional √2 =1,41421356…. con infinitas cifras decimales no periódicas
Primero: Probar que √2 es un número irracional
Demostración: Supongamos que existen dos enteros a y b primos entre si tales que (√2 es igual a la fracción irreducible:
![]() Elevando al cuadrado:
Elevando al cuadrado:
2 b2 = a2 (1) ⇒ a2 par ⇒ a par ⇒ a = 2 a’
2 b2 = (2 a’)2 ⇒ 2 b2 = 4 a’2 ⇒ b2 = 2a’2 ⇒ b2 par ⇒ b par
Con lo que la fracción a/b no es irreducible, ya que a y b son divisibles por 2.
Segundo: La apariencia más o menos compleja de los radicales no indica su irracionalidad aquí hay dos ejemplos de expresiones complejas que en realidad son números enteros
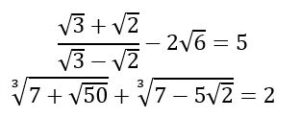
Tercero: Demostrar que es irracional el número:
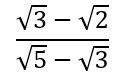
Demostración: Supongamos que existe r racional tal que
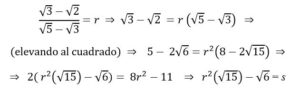
(Donde s = (8r2 – 11)/2 es otro número racional)
Elevando al cuadrado:
15 r4 + 6 – 2 r2 √90 = s2 ⇒ √ 90 = 3 √10 = (15 r4 – s2 + 6)/ 2r2
√10 = (15 r4 – s2 + 6)/6 r2
Lo que es absurdo, ya que √10 un número irracional y (15 r4 – s2 + 6)/6 r2 es un número racional.
Cuarto: Demostrar que log4 18 es un número irracional
Demostración : Utilizaremos las propiedades del logaritmo del producto de dos número y el cambio de bases de los logaritmos:

Basta probar que log2 3 es irracional: Si log2 3 fuera racional, existiría a y b enteros tales que:
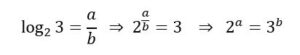
Absurdo, ya que 2 a es un numero par y 3b es impar.




