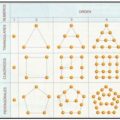
PROBLEMA 1. Dado un entero k >l, definimos ak como el número entero que en base diez se escribe: 11…k …1= ak (es decir, ak tiene sus k cifras todas iguales a 1) Demostrar que ak divide a al si y sólo si k divide a l.
Solución: Basta reparar en que:
a6:a2 = 111111 : 11 = 11(1+100+10000) = a2(1+102+104)
a11:a3 = 11111111111 : 111 = 111(1+103+106) = a3 (1+103+106) +11
Si l = dk + r donde r < k, entonces
al = ak 10r· (1+ 10k + 10 2k + ···10(d-1)k + ar
(Como a0 = 0.) Si k divide a l será r = 0 y es evidente que ar = 0 de forma que ak divide a al . Recíprocamente, si ak divide a al entonces debe ser ar =0 y por tanto r = 0.
PROBLEMA 2: Sean a, b, c, d números enteros positivos que satisfacen ab = cd. Demostrar que a + b + c + d no es un número primo.
Solución:
Usaremos la hipótesis ab = cd y multiplicaremos (a +b + c + d) por uno de sus sumandos, por ejemplo: b
b (a +b + c + d) = ba+ b2 + bc + bd = [como ba = cd)
= cd+ b2 + bc + bd = b(b+c) + d(b+c) =
= (b+c)(b+d),
Por lo tanto b (a +b + c + d) = (b+c)·(b+d)
Si (a + b + c + d) fuese primo debería dividir a (a + c) o (a + d) que son menores que él, lo que es absurdo. ¿Se podría asegurar este resultado si a, b, c, d números enteros cualesquiera?
PROBLEMA 3 Halla todos los pares de números naturales x, y (x < y) tales que la suma de todos los números naturales comprendidos estrictamente entre ambos es igual a 1999.
Solución:
Tenemos que sumar del número x+1 hasta el número y – 1 ambos incluidos y que la suma de todos ellos sea 1999. Es la suma de los términos de una progresión de aritmética de y – x – 1 términos cuya diferencia es 1
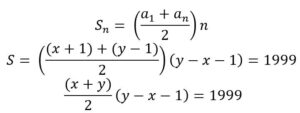
Que llegamos a: (x + y) (y – x– 1) = 2·1999 (1)
Teniendo en cuenta que los números x e y son positivos por ser naturales, que (x+y) > (y – x –1) y que 2 y 1999 son números primos caben dos posibilidades para la ecuación (1):
Primera: Que x + y = y que y – x –1=1999 ⇒ (resolviendo el sistema) x = 1998 e y = 2000, entre ellos sólo está el número 1999 (Progresión aritmética de un solo término). El par x, y es 1998 y 2000
Segunda: Que x + y = y que y – x –1= 2 ⇒ (resolviendo el sistema) x = 998 e y = 1001, entre ellos están el número 999 y 1000 (Progresión aritmética de dos términos). El par x, y es 998 y 1001
PROBLEMA 4.-. ¿Cuál es el exponente de 7 en la descomposición de 2025! en producto de factores primos?
Solución: De 1 a 2025 el número de múltiplos de 7 será: La parte entera de (2025 /7), que escribiremos: Ent (2025/7) = 289
Los múltiplos de 72, aportan dos sietes, luego habrá que añadir un número de sietes igual a: Ent (2025/72) = 41.
Igualmente habrá que añadir un siete más por los múltiplos de 73, que es: Ent (2025/73) = 5. Finalmente, Ent (2025/74) = 0.
Por tanto, el exponente de 7 en 2025! es: 289 + 41+ 5 = 335