Se llama arco capaz de ángulo X de un segmento AB al lugar geométrico de los puntos del plano desde los que observa el segmento AB bajo un ángulo X
El arco capaz está relacionado con la forma de la disposición de las butacas de un teatro desde las que se puede observar el escenario bajo el mismo ángulo.
Un ejemplo de arco capaz es la semicircunferencia, la cual es el arco capaz de 90º del diámetro AB. Ya que, desde cualquier punto de la semicircunferencia se puede observar el diámetro bajo un ángulo de 90º
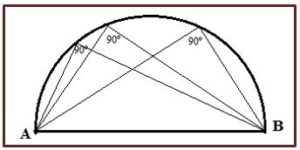
Los problemas de cálculo del arco capaz están relacionados con las propiedades de los ángulos inscritos en una circunferencia que subtienden la misma cuerda AB. Sabemos que los ángulos inscritos en la circunferencia la mitad del arco que abarcan sus lados o, lo que es igual: la mitad del ángulo central correspondiente.
Construcción del arco capaz de ángulo x de un segmento AB:
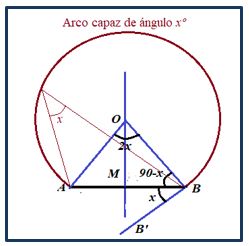
Sea el segmento AB si el ángulo x < 90º,
- Se traza la mediatriz de AB, MO
- Se dibuja el ángulo x = ABB’ con vértice en el extremo B del segmento.
- Se levanta una perpendicular a BB’ por el punto B que corta a la mediatriz de AB en el punto O.
- El punto O es el centro del arco capaz
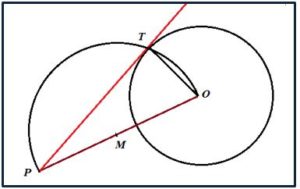
Aplicación al dibujo técnico: (para determinar la tangente a una circunferencia de centro O desde un punto P). Como la tangente a una circunferencia y el radio que pasa por el punto de contacto son perpendiculares, podemos usar el arco capaz de 90º.
Determinaremos el arco capaz de 90º (semicircunferencia) de diámetro el segmento de extremos el punto P, desde el que queremos trazar la tangente, y el centro O de la circunferencia. El punto T de intersección de la circunferencia de centro O y la semicircunferencia será el punto de tangencia buscado y la recta PT es la tangente buscada.
Ejercicio de localización en el mar: Desde un barco P se observan tres faros situados en la costa A, B y C, midiendo el ángulo bajo el que se ven resultan 50º para A y B, y 60º para B y C. Situar la posición del barco en el mar.
Basta con dibujar el arco capaz de 50º del segmento AB y el arco capaz de 60º del segmento BC, como se indica en la figura. El punto P, intersección de ambos arcos, es el punto en el que se encuentra el barco

Este ejercicio tiene una bonita redacción situando el emplazamiento del barco en las proximidades de la Manga del Mar Menor. En: https://almargendefermat.wordpress.com/2009/08/26/navegando-con-el-arco-capaz/
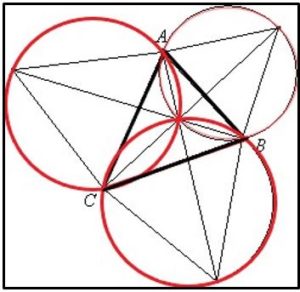
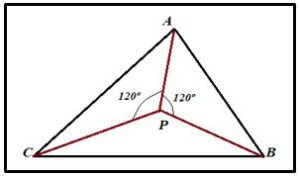
Determinar el punto de Fermat de un triángulo cualquiera ABC. Debemos recordar que el punto de Fermat es un punto P cuya suma de distancias a los vértices del triángulo es mínima (PA + PB + PC mínima) y cumple que ang (APB) = ang(BPC) = ang(APC)= 120º
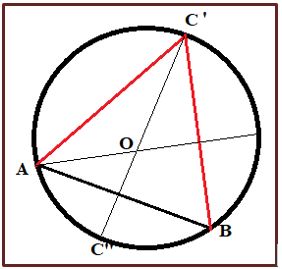
Esbozaremos otra forma de calcular el arco capaz de 60º (o de su suplementario, 120º) que consiste en dibujar un triángulo equilátero de lado AB, según se muestra en la figura. Los puntos de la circunferencia que están en el lado de C’ forman parte del arco capaz de 60º y los que están en el lado de C’’ forman parte del arco capaz de 120º.
Haciendo la misma construcción sobre cada uno de los lados del triángulo la intersección de los tres arcos capaces de 120º nos da el punto P de Fermat.