
Cuando hablamos de caos determinista estamos asociando dos términos de significado muy diferente. El caos lo asociamos con desorden, con el azar, con lo imprevisible y con lo que no obedece unas reglas, mientras que el determinismo es una postura filosófica que mantiene que nada ocurre por azar, que todos los sucesos se producen por una o varias causas determinadas, que la mente humana puede descubrir. La ciencia, con su capacidad de hacer predicciones, es se ha considerado una prueba del comportamiento determinista del mundo.
Los antiguos griegos concebían el caos como una inmensidad vacía que había precedido a la formación del Universo. Según Hesíodo (hacia el 700 a. C.) al principio del mundo sólo existía el Caos del que surgieron diferentes generaciones de dioses que dirigieron el complicado proceso que va desde Caos primordial, caracterizado por ausencia de orden, al Cosmos concebido como un todo ordenado, Ovidio (43 a.C. – 17 d.C.) en las Metamorfosis identifica al Caos como desorden esencial.
Por otra parte, el determinismo es un concepto de muchas caras, relacionado con el fatalismo, que se asocia como algo anulador de los deseos de libertad del hombre; el fatum eliminaba nuestra libertad, porque el destino actuaba como una corriente que arrastraba todo lo que sucedía y los condicionaba todo, hasta nuestro pensamiento. Dentro de esta corriente de pensamiento, cuando nuestra mente analiza las manifestaciones que preceden a un suceso y descubre que las mismas situaciones previas, en las mismas condiciones, producen los mismos efectos se llega a un conocimiento causal. Este conocimiento nos lleva establecimiento de Leyes Físicas, a las que ascendemos de categoría cuando las consideramos como normas que gobiernan el comportamiento del mundo físico.
El mundo mecanicista en el que nació la Ciencia Moderna no era determinista, de hecho los grandes científicos como G. Galilei (1564-1642), R. Descartes (1596-1650), I. Newton (1642-1717) , L. Euler (1707-1783) , etc. no lo eran. Pero, por el camino que abrieron, se obtuvieron unas leyes que predecían el movimiento de los astros, la localización de nuevos planetas e incluso a se llegó a demostrar con ellas la estabilidad del Sistema Solar. En suma, unas leyes que adivinaban el futuro. Esto hizo que apareciera una corriente filosófica que, rebasando el alcance de los descubrimientos científicos, pensaran que todo lo que sucedía estaba preparado y determinado desde el principio, formulando lo que se conoce como determinismo científico. Un modelo determinista producirá siempre la misma salida a partir de las mismas condiciones de partida o el estado inicial.
El determinismo científico del siglo XVIII está representado por el astrónomo y matemático P. S, Laplace (1749-1827), que, aplicando las leyes de la Mecánica Celeste de Newton, reformuladas por Euler y J.L. Lagrange (1736-1813), llegó a postular la previsibilidad ilimitada, precisa e inequívoca de los sucesos. Laplace había formulado unas leyes deterministas expresadas en términos de Ecuaciones Diferenciales que pensaba que devolvían siempre el mismo resultado para un conjunto específico de valores iniciales de entrada.
Laplace, en el prefacio de su obra Théorie analytique des probabilités (1812), expresó la forma más conocida determinismo científico de la Naturaleza derivada del sistema newtoniano. Aseguraba que conociendo perfectamente las condiciones iniciales en el momento presente y, mediante el cálculo matemático, se podría llegar a conocer cómo habían sido situaciones pasadas y cómo serán las situacines del futuro. A esa inteligencia calculadora, capaz de aplicar las fórmulas, se le ha conocido como el demonio de Laplace. Laplace decía:
“Es nuestro deber considerar el estado actual del universo como un efecto de su anterior estado y como la causa de uno que lo sucederá. Si fuera posible tener por un instante una inteligencia que pudiera abarcar todas las fuerzas que animan a la Naturaleza y la situación respectiva de los seres que la componen – una inteligencia lo suficientemente enorme como para someter al análisis estos datos – comprendería en la misma fórmula el movimiento de los cuerpos más grandes del universo y el del átomo más liviano; para ella nada sería incierto y el futuro, así como el pasado, se presentaría ante sus ojos”.
Creer en un universo determinista es creer en que aunque, por nuestras limitaciones, no podamos predecir todas las situaciones circunstancias de una situación determinada, es posible predecir el futuro. Sin embargo, la complejidad de las ecuaciones era tan grande que nuestra capacidad para predecir el futuro estaba limitada en la práctica.
Pero hubo un hecho que dio en la línea de flotación de la creencia determinista y fue el descubrimiento de que algunas ecuaciones se mostraban muy sensibles a las condiciones iniciales y, en ellas, un pequeño cambio en las condiciones iniciales podía provocar una perturbación muy grande en los resultados; este fenómeno, aunque hubo antecedentes con el estudio del problema de los tres cuerpos, estudiado a finales del siglo XIX por H. Poincaré (1854-1912), fue descubierto a mediados del siglo XX y se denomina Caos Determinista.
Con las leyes de Newton se había conseguido resolver el problema de los dos cuerpos sometidos a atracción gravitacional mutua (el Sol con un planeta) y se había determinado, a partir las ecuaciones diferenciales asociadas, que los planetas sometidos a la Ley de Gravitación Universal, describían órbitas elípticas alrededor del Sol e igualmente la órbita de los movimiento de un satélite respecto a su planeta.
El problema de los tres cuerpos plantea el estudio de cómo sería la órbita, si en lugar de contar con dos cuerpos en forma aislada, aparece un tercer cuerpo perturbando el sistema. Se trata de determinar calcular las posiciones y las velocidades de tres cuerpos masivos en cualquier instante sometidos a la Ley de Gravitación Universal, conociendo las posiciones y las velocidades de los tres en un momento dado. Sería, por ejemplo, estudiar la órbita de la tierra si, además, de la atracción Solar consideramos la influencia atractiva de la Luna.
La solución del problema se resistía y preocupaba a la comunidad científica y el Rey 1884 en Oscar II de Suecia (1829-1907) convocó, con motivo de las celebraciones de sus sesenta cumpleaños un concurso con un sustancioso premio para el que resolviera el Problema de los Tres Cuerpos, el anuncio del premio se publicó en la revista Acta Mathematica en 1885, y de los trabajos se debían presentar antes de junio de 1888.
H. Poincare participó en el concurso y en su trabajo Mémoire sur les Courbes Définies par une Équation Différentielle descubrió que el problema no tenía solución, porque el sistema de ecuaciones diferenciales no lineales que se planteaban a partir de las ecuaciones de Newton era muy sensible a las condiciones iniciales. Es decir, que pequeñas variaciones en los datos de entrada podían producir grandes variaciones en los resultados finales. El matemático francés siendo declarado ganador por el jurado en el que figuraba el gran matemático K. Weirstrass (1815-1897).
La conclusión principal de Poincaré en su trabajo fue que las órbitas de los cuerpos obtenidas mediante las ecuaciones de Newton eran caóticas en las que pequeñas variaciones tan pequeñas como las debidas a pequeños errores de medición en las condiciones iniciales, conducían a resultados muy diferentes.
Esto se debía a que el problema no tenía una solución analítica, es decir, que no existe una solución en términos de las funciones usuales como, polinomios de cualquier grado incluso fraccionario, funciones trigonométricas, exponenciales o logarítmicas. Aunque fuera posible calcular y las órbitas mediante aproximaciones numéricas con el grado de precisión que se desee.

En 1960 el meteorólogo del Instituto Tecnológico de Massachusetts (MIT). E. Lorenz (1917-2008), descubrió, haciendo predicciones del tiempo, un sistema de ecuaciones, que era muy sensible a las condiciones iniciales. El sistema de Lorenz era un sistema autónomo no lineal de ecuaciones diferenciales ordinarias dado por:
x’(t) = σ·(y(t) – x(t))
y’(t) = r·x(t) – y(t) – x(t)z(t)
z’(t) = x(t)y(t) – b·z(t)
donde σ > 0, r > 0 y b > 0 son parámetros.
Las variables que Lorenz utilizaba en su sistema eran:
x(t) magnitud proporcional a la intensidad del movimiento convectivo,
y(t) magnitud proporcional a la diferencia de temperatura entre la corriente ascendente y la descendente.
z(t) magnitud proporcional a la desviación de la temperatura vertical respecto al valor de equilibrio.
Lorenz calculó las soluciones numéricas del sistema para los valores de los parámetros:
σ = 10, r = 28, b = 8/3. Es decir, para el sistema:
x´(t) = 10(y – x)
y´(t) = 28x – y- xz
z´(t) = xy – 8x/3
para dos valores iniciales de las variables muy próximos. En la gráfica siguiente se muestra en azul la solución de x para la condición inicial (x0, y0, z0) = (7, 7, 7) y en verde la solución de x para condición inicial (x0, y0, z0) = (7’001, 7, 7)
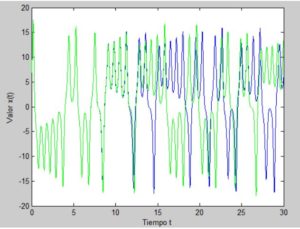
Se puede observar que al principio las soluciones con ambas condiciones iniciales coinciden, pero, a medida que pasa el tiempo los resultados comienzan a diferir hasta alcanzar valores opuestos. Esta es la razón de que las predicciones meteorológicas no sean fiables para largos periodos de tiempo. Esto significa que cualquier variación se amplificará más y más hasta hacer que el resultado obtenido mediante la resolución numérica de un sistema no lineal no sea fiable. Este fenómeno se conoce como «efecto mariposa” que se suele expresar en la forma: el movimiento de las alas de una mariposa en Brasil puede provocar un tornado en Tejas.
El caos determinista ha aparecido en las ecuaciones diferenciales no lineales. Uno de las más más conocidas es la ecuación logística, que fue popularizada en 1976 por el biólogo Robert May en su artículo Modelos matemáticos sencillos con dinámicas muy complicadas.




