
Contar las cifras de un número cuando está escrito es fácil. Es más complicado decir cuantas cifras de una potencia tendrá una potencia sin calcularla y bastante más complicado calcular las cifras del factorial de un número n!, siendo
n! = n·(n-1)·(n-2) ··· 3·2·1
El significado de n! es el número de ordenaciones que se pueden hacer con los elementos de un conjunto de n elementos distintos y es un número muy grande aunque n no lo sea, así:
8! = 40.320 10! = 3.628.800 12! = 479.001.600
Podemos preguntarnos calcular 1000!. Indudablemente, será un número enorme. En este trabajo trataremos de conocer cuántas cifras tiene. Para ello situaremos a 1000! entre dos potencias sucesivas de 10.
Dado un número natural a, puede ocurrir que 100 ≤ a < 10 1, entonces a tiene una cifra; mientras que si 101 ≤ a < 10 2, a tendrá dos cifras y si 102 ≤ a < 10 3, entonces a tendrá tres. En general, si un número natural a tiene x cifras estará situado 10x-1 ≤ a < 10 x ⇒ x – 1 ≤ log a < x y recíprocamente.
Lo que significa que log a es un número decimal cuya parte entera es x – 1. Luego podemos concluir que:
x = (Nº de cifras decimales de un número natural a) = Ent (log a) +1
Este resultado puede servirnos para calculas las cifras de cualquier potencia, como vemos a continuación:
Ejercicio 1: ¿Cuántas cifras tiene el número 139?
Respuesta: Nº de cifras de 139 = Ent (log 139) + 1 = Ent (9·log 13) + 1 =
= Ent (10,025) + 1 = 10 + 1 = 11 cifras
Ejercicio 2 : ¿Cuántas cifras tiene el número 1523·2391?
Respuesta: Nº de cifras de 1523·2391 = Ent [log (1523·2391)]+ 1 =
Ent [23·log 15+ 91· log 23] + 1 = Ent [27,05+123,92] + 1 = Ent [150,97] + 1 = 151 cifras
Este método que resulta bueno para potencias, pero no lo es tanto para factoriales, porque los factores son diferentes.
Ejercicio 3 : ¿Cuántas cifras tiene el número 10!?
Respuesta: Ya hemos calculado multiplicando 10! (son siete cifras). Podemos seguir aplicando la regla anterior, pero habría que calcular la suma de logaritmos y la tarea resultaría tediosa.
Nº de cifras de10!= Ent (log 10!) + 1 =
= Ent (log 10 + log 9 + log 8 + ···+ log 2+ log 1) +1 = Ent (1 + 0,954242 + 0,903090 +
+ 0,848509 + 0,778115 + 0,698970 + 0,602060 + 0,477121 + 0,301030) + 1 = 6 +1 =7
El procedimiento se hace más laborioso cuanto mayor sea el número del que calculamos el factorial.
Hay un procedimiento mejor que permite acotar el número de cifras de forma más eficiente por grande que sea el número del que calculemos el factorial. El método consiste en utilizar el cálculo integral. Así, en lugar de hacer una suma de muchos sumandos, realizamos una integral definida y acotamos con ella la suma de los logaritmos.
Aplicaremos la idea para acotar inferior y superiormente el número de cifras de 8! Que serán:
x = Nº de cifras de 8!= Ent (log 8!) + 1 = Ent ( log 8 + log 7 + ···+ log 2) +1
En la gráfica siguiente se representan siete rectángulos de áreas log 2, log 3, ··· log 8. La suma de las áreas de estos rectángulos está acotada inferiormente por el área limitada por la curva: y = log x y el eje OX entre x = 1 y x = 8
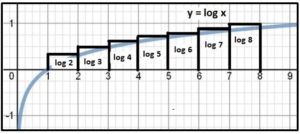
Por lo tanto se cumplirá que:
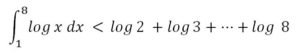
En la gráfica siguiente se representan siete rectángulos de áreas log 2, log 3, ··· log 8. La suma de las áreas de estos rectángulos está acotada superiormente por el área limitada por la curva: y = log x y el eje OX entre x = 1 y x = 9

Por lo tanto se cumplirá que:
Por lo tanto, combinando ambos resultados: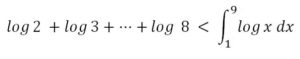
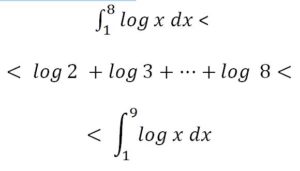
Esta fórmula se puede generalizar sin dificultad a n!
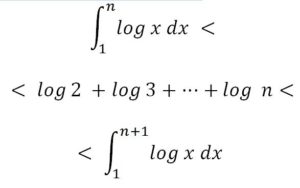
Integrando (para lo que cambiaremos a logaritmos neperianos): log x = Ln x/Ln 10:
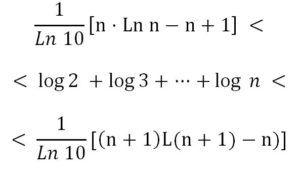
Si queremos calcular el número de cifras de 1000! (haciendo n=1000)
Teniendo en cuenta que:
x = Nº de cifras de 1000!= Ent (log 1000!) + 1 = Ent ( log 1000 + log 999 + ···+ log 2) +1
Se tiene que:

Lo que da que 2567 < Nº de cifras de 1000! < 2570
Que es una acotación bastante aceptable, ya que el número de cifras de 1000! es 2568

