Reflexionaremos un poco sobre un problema geométrico sencillo y compararemos la resolución del mismo por métodos algebraicos próximos a la Geometría Analítica con la solución del mismo mediante la Geometría Clásica, que resuelve los problemas mediante construcciones geométricas que pueden realizarse con la regla y el compás
El problema que vamos a resolver es: Determinar el lado de un cuadrado inscrito en un triángulo cualquiera.
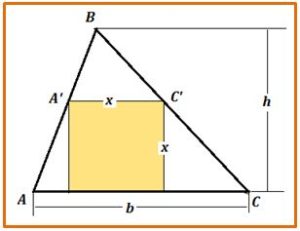
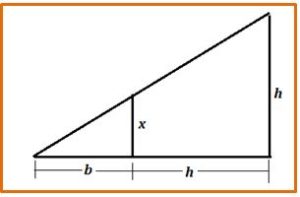
Para resolverlo siguiendo los métodos de la geometría cartesiana supondremos que el problema está resuelto con el cuadrado ya inscrito tal y como se muestra en la figura, en la que se observa que el triángulo ABC es semejante al triángulo A’BC’. Por lo tanto, tomando AC = b, como base del triángulo y la distancia del vértice B a la base como altura, h, del mismo, si llamamos x al lado del cuadrado inscrito, se tiene que:
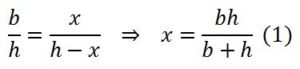
Con este cálculo, conociendo las medidas de la base y la altura del triángulo, podemos calcular la medida del lado del cuadrado inscrito.
La Geometría Clásica disponía de hermosos procedimientos constructivos para resolver este tipo de problemas. Consideremos el problema de construir un cuadrado inscrito en un triángulo equilátero. Para construir el cuadrado inscrito en un triángulo equilátero se podía emplear una homotecia, siguiendo los siguientes pasos:
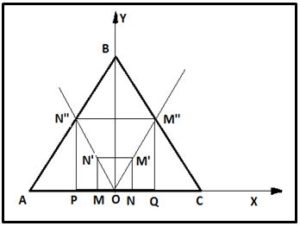
1.- Dibujamos en la base AC = b del triángulo un cuadrado de tamaño cualquiera, con un lado sobre la base y simétrico respecto al la altura BO, por ejemplo, MNM’N’.
2.- Desde O, punto medio de la base AC, trazamos las rectas ON’ OM’, que cortan a los otros dos lados del triángulo equilátero en N’’ y M’’.
3.- El cuadrado PQM’’N’’ es el cuadrado buscado
De la fórmula (1) obtenida anteriormente, teniendo en cuenta que si L es el lado del triángulo la altura será h = L√3/2.
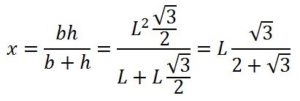
Volviendo al caso general del cuadrado inscrito en un triángulo cualquiera, la Geometría Clásica, tiene diferentes construcciones para resolverlo, teniendo en cuenta que la expresión (1) se puede expresar en la forma: b·h = x·(b+h). Donde b·h es el área de un rectángulo de base b y de altura h altura (de doble área que el triángulo) que es igual al área de otro rectángulo de base b+h y altura x.
Pero consideraremos la relación en la forma:
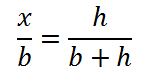
Y dibujaremos x teniendo en cuenta que calculamos un cuarto proporcional entre b, h y b+h es decir que guasta la relación indicada en forma gráfica a continuación:
Que en el dibujo sobre el triángulo:
Paso 1.- Prolongar la base, AC = b, del triángulo ABC una longitud igual a la altura h del triángulo de modo que CK = h.
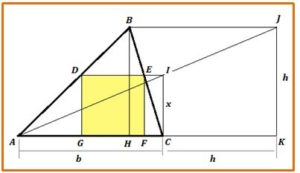
Paso 2.- En el punto K levantamos una perpendicular KJ = h.
Paso 3 Trazamos una recta AJ y una perpendicular y levantamos una perpendicular a la base por el punto C hasta cortar a AJ en el punto I.
El segmento CI =x y será el lado del cuadrado que buscamos.
Paso 4.- Desde el punto I trazamos una paralela a la base que corta a los lados BC y BA en E y D respectivamente.
Paso 5.- Desde E y D trazamos sendas perpendiculares a la base que determinan en ella los puntos F y G respectivamente.
DEFG es el cuadrado inscrito en el triángulo ABC.