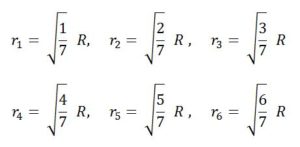
Cuando pensamos en dividir un círculo en n partes de igual área pensamos en partirlo en n sectores de graduación 360º/n. Este problema es equivalente al de construir de polígonos regulares de n lados Los griegos se propusieron resolver este problema utilizando solamente la regla y el compás.
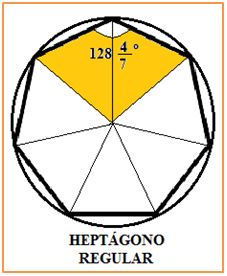
Consiguieron construir con regla y compás el triángulo equilátero, el cuadrado, el pentágono regular y el hexágono, pero el heptágono regular se resistía; no se encontró un procedimiento con el que construirlo con esos instrumentos.
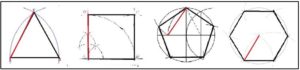
Desde hacía más de 2000 años, se sabía cómo construir con regla y compás el triángulo equilátero, el cuadrado y el pentágono regular y, a partir de ellos, se podían construir por bipartición otros polígonos regulares de seis ocho diez o doce lados. Pero no se había conseguido construir un polígono regular con un número primo de lados, siete, once, trece, diecisiete o diecinueve… Tampoco polígono de nueve lados o el de doce.
Pero, en 1796, K.F.Gauss (1777-1855) hizo un brillante descubrimiento; desarrolló un método para construir con la ayuda de regla y compás el heptadecágono regular, polígono regular de diecisiete lados. Además, demostró el número de lados que debían tener los polígonos regulares que se podían construir con ayuda de regla y compás: la descomposición en n partes se podía hacer en los siguientes casos:
- Caso 1.- Cuando n = 2r, siendo r un número natural, es decir, se podían construir polígonos de cuatro, ocho, dieciséis, treinta y dos lados, …
- Caso 2.- Cuando n era un primo de Fermat. Un primo de Fermat es un número primo de la forma n = 2r + 1 siendo r una potencia de dos, es decir:
![]()
- Caso 3.- Cuando n era producto de números del tipo anterior, es decir, el producto de una potencia de dos por un primo de Fermat; el producto de varios primos de Fermat diferentes; o el producto de una potencia de dos por varios primos de Fermat diferentes.
![]()
Siendo r un número natural y los pi números primos de Fermat distintos.
El heptadecágono o polígono regular de 17 lados podía ser construido con regla y compás por ser 17 = 24 +1 un número primo de Fermat. Pero no podían ser construidos el heptágono (siete no es potencia de dos no primo de Fermat), ni el eneágono (nueve es producto de dos primos de Fermat iguales), ni el endecágono (once no es primo de Fermat). Sin embargo podrían construirse con regla y compás los polígonos regulares de 257 y 65537 lados, ya que eran primos de Fermat.
257 = 28 + 1 y 65537 = 216 + 1
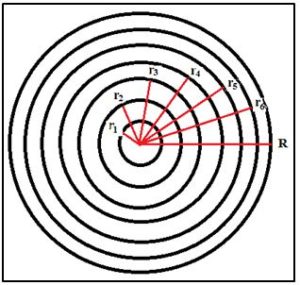
Aunque un círculo no se puede dividir en siete, once o nueve sectores iguales utilizando la regla y el compás, si se puede dividir en siete partes de la misma área con forma de corona circular.
Tomando como ejemplo el heptágono, podemos construir un círculo concéntrico que renga un área igual a a/7 del área del círculo dado de radio R. Sea su círculo ra, entonces :
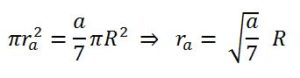
Entonces para calcular el radio de un círculo de cuya área sea a/7 del área de un círculo dado de radio R basta con saber construir, a partir de a:
![]()
Que son cosntruibles con regla y compás, resulltando: