Dividir una figura geométrica en partes iguales siguiendo sus líneas fundamentales, ya sean alturas, diagonales, medianas o aprovechando sus propiedades de simetría, es una fuente de ejercicios fácilmente comprensibles de la geometría elemental.
La fórmula que permite calcular el área del triángulo como la mitad del producto de la base del mismo por su altura correspondiente nos permite plantear una serie de ejercicios
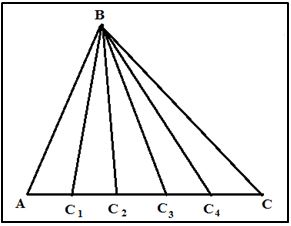
Ejercicio 1.- Dividir y triángulo ABC en cinco triángulos de igual área.
Solución: Si tomamos como base el lado AC las altura del triángulo será la perpendicular desde el vértice B hasta la base. Dividimos la base AC en cinco partes iguales por los puntos C1, C2, C3, C4, entonces los triángulos BAC1, BC1C2, BC2C3, BC3C4, BC4C, tienen la misma área, ya que sus bases son iguales (AC1= C1C2= C2C3= C3C4= C4C) y su altura es común (la distancia de B a AC).
Problema 2.- Construir un triángulo con la misma área que un cuadrilátero.
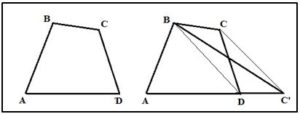
Solución: Dado un cuadrilátero ABCD para construir un triángulo ABC’ que tenga la misma área que él. Procederemos de la siguiente forma: quitaremos al cuadrilátero ABCD el triángulo BCD y le añadiremos otro que tenga la misma área que él y que uno de sus lados sea prolongación del lado AD del cuadrilátero.
Trazamos la diagonal BD y prolongamos el lado AD.
Trazamos un paralela a la diagonal BD que pase por el vértice C. Esta paralela cortará a la prolongación de AD en C’.
El área del triángulo BDC (que le quitamos al cuadrilátero) tiene la misma área que el triángulo BDC’, ya que ambos tienen la misma base (la diagonal BD) y la misma altura, ya que sus vértices opuestos respectivos están en una recta paralela a BD. Por lo tanto el cuadrilátero ABCD tiene la misma área que el triángulo ABC’.
Problema 3.- Las diagonales de un cuadrilátero lo dividen en cuatro triángulos. Si se conocen las áreas de tres de esos triángulos (10u2, 30u2 y 24u2) calcula el área del cuadrilátero
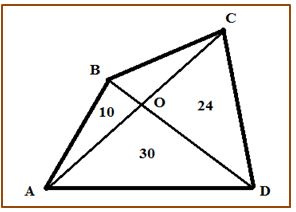
Solución: Representemos la situación en la siguiente figura. Si tomamos como línea base la diagonal BD, los triángulos ABO y ABO tienen la misma altura h, que será la perpendicular trazada desde el vértice A hasta la base BC , es decir:
Altura de (ABO) = altura de (ADO) = h ⇒
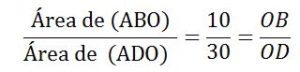
Por lo tanto: OD= 3OB.
Igualmente, los triángulos CBO y CDO tienen la misma altura h’ que será la perpendicular trazada desde el vértice C hasta la base BC:
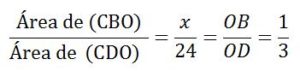
x =Área de (ABO) = 8u2.
Luego el área del cuadrilátero será: 10 + 30 + 24 + 8 = 72u2
Problema 4.- Las bases de un trapecio isósceles miden 8u y 12 u. Las diagonales lo dividen en cuatro triángulos, dos de los cuales miden 24u2. Calcula su área.
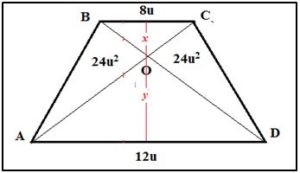
Solución: Los triángulos OAD y OBC son semejantes, de razón de semejanza 12/8 = 3/2, por lo que x = 3y/2, entonces se verifica:
Área del Trapecio = Área OAB + Área OBC + Área OCD + Área ODA =
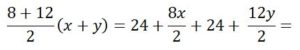
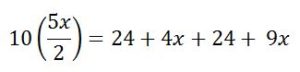
⇒ 25 x =13x + 48 ⇒ 12 x = 48 ⇒ x = 4 e y = 6 ⇒ altura =10 ⇒
![]()