
El análisis matemático de las posibilidades de ganar en los juegos de azar comenzó con la Ciencia Moderna. A mediados del siglo XVI, G. Cardano (1501-1576) escribió un libro sobre el tema, pero que fue descubierto por la comunidad científica un siglo después de su muerte, cuando ya se habían publicado estudios que iban más allá de donde había llegado el matemático italiano, por lo que la obra de Cardano apenas tuvo repercusión. En 1656 Chr. Huygens (1629-1695) publicó un tratado titulado De Ratiociniis in Ludo Aleae (Sobre el cálculo en los juegos de azar). Huygens conocía la correspondencia que intercambiaron los matemáticos franceses B. Pascal (1623-1662) y P. Fermat (1601-1665) en la que se planteaban, entre otros un problema planteado por el caballero De Méré sobre los juegos de azar, el problema del reparto de apuestas cuando se suspendía una partida y el libro de Huygens siguió la línea de estos grandes científicos.
Huygens introdujo la noción de Esperanza Matemática, también denominada valor esperado. La esperanza permitía determinar si un juego era justo, favorable o desfavorable para un jugador. Para Huygens consistía en determinar, si se jugaran N partidas, el número de jugadas que podía esperar ganar cada jugador.
PROBLEMA: Un jugador y yo lanzamos alternativamente dos dados con la condición de yo habré ganado cuando la suma de las puntuaciones obtenidas en ambos sea siete puntos y él cuando ganará cuando la suma sea seis. Si él lanza primero calcular la relación entre su esperanza y la mía.
Solución: Pensemos en dos dados diferentes. Los resultados de cada tirada con los dos dados de dos (cuando sale (1,1)), tres cuando sale (1,2) y (2,1), … hasta doce (cuando sale (6,6)).
El siete puede salir de seis formas diferentes (1,6) (6,1), (1,5), (5,1), (3,4), (4,3) y el seis de cinco maneras: (1,5) (5,1) (2,4) (4,2) (3,3). Como hay 36 posibles resultados distintos:
![]()
Como mi contrincante juega en primer lugar, La primera posibilidad de ganar la tiene en la primera jugada sacando seis, si no ha obtenido un seis en la primera, en la segunda posibilidad la tiene cuando yo no obtengo siete y la saca un seis en su segundo lanzamiento, lo que da un conjunto indefinido de posibilidades mientras yo no obtenga siete, que esquematizamos así:
Primera: (6), Segunda: (no 6)(no7) y (6), Tercera: (no 6)(no7)(no 6)(no7)(6),
Cuarta: (no 6)(no7)(no 6)(no7) (no 6)(no7)(6), …., y así sucesivamente
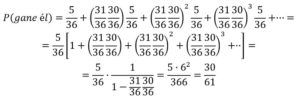
Por otra parte:
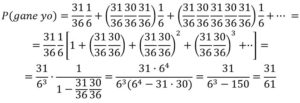
La esperanza es 31 a 30 a mi favor
PROBLEMA: Tres jugadores A, B y C toman doce fichas, de las cuales cuatro son blancas y ocho negras. Acuerdan que ganará el primero que, escogiendo a ciegas, saque una ficha blanca. En el juego acuerdan que A elegirá primero, luego B y después C, luego volverá a elegir A y así sucesivamente por turno. Calcula la relación entre sus esperanzas. (suponemos que en cada extracción se repone la ficha)
Solución: En cada extracción la probabilidad de ganar de cada jugador será 4/12 = 1/3 y de perder 8/12 = 2/3
Designaremos con A, que gane A en una extracción, y con A’ que pierda. Igualmente, B significa que gane B en una extracción y B’ que pierda y, finalmente, indicaremos con C, que gane C en una extracción y con C’ que pierda.
El jugador A puede ganar en las siguientes situaciones:
Primera: A, Segunda: A’B’C’A, Tercera: A’B’C’A’B’C’A,
Cuarta: A’B’C’A’B’C’ A’B’C’A,…, y así sucesivamente.
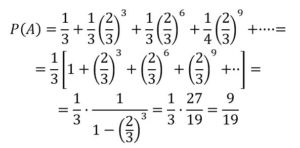
El jugador B puede ganar en las siguientes situaciones:
Primera: A’B, Segunda: A’B’C’A’B, Tercera: A’B’C’A’B’C’A’B,
Cuarta: A’B’C’A’B’C’A’B’C’A’B,…, y así sucesivamente
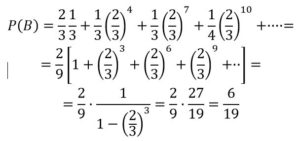
Jugando un gran número de veces, n, por ejemplo, 19.000, A ganará 9,000 veces, B ganará 6.000 veces y C 4.000 veces.

