
Con seguridad, el mejor camino para despertar la curiosidad a un estudiante consiste en ofrecerle un juego intrigante, un puzle, un truco de magia, un chiste o una paradoja de naturaleza matemática. Martin Gardner (1914- 2010)
Un juego sencillo en el que se relacionan de forma elemental el manejo de números y el descubrimiento de estrategias ganadoras es el del montón de cerillas.
El juego consiste en colocar a dos jugadores frente a un montón con un número de cerillas N conocido por ambos jugadores. Cada jugador debe retirar alternativamente un número de cerillas menor o igual que un número n y ganará el jugador que se lleve la última cerilla.
Cuando los dos jugadores se disponen a jugar se hacen las siguientes preguntas ¿Hay alguna estrategia para ganar el juego? ¿Tiene siempre ventaja el jugador que comienza? ¿Influye en la victoria de los jugadores la relación entre el número de cerillas, N, del montón y el número máximo de cerillas, n, que puede retirar cada jugador en su turno?
Analizaremos el juego con el siguiente ejemplo numérico:
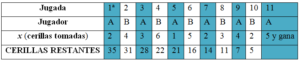
Dos jugadores, A y B se encuentran ante 37 cerillas sobre una mesa. Cada uno de ellos jugador tomará alternativamente, de una a seis cerillas y el juego lo ganará el que se lleve la última cerilla.
Para hallar la estrategia ganadora de un jugador analizaremos el juego a partir de la última jugada. Un jugador, por ejemplo el A, ganará si en la última jugada se encuentra con seis cerillas o menos, de ese modo puede llevarse todas y, por tanto, tomar última cerilla. Por lo tanto, en su penúltima jugada, el jugador A le debe dejar al jugador B siete cerillas. Es fácil ver que en la antepenúltima A le debe dejar a B, 14 cerillas, en la anterior 21 y así sucesivamente. Es decir que, en cada ocasión el jugador A le tiene que dejar a B un número de cerillas que sea múltiplo de siete.
Esto es, la sucesión 7, 14, 21, 28 y 35. Por lo tanto, la estrategia ganadora del jugador A, cuando se encuentra ante las 37 cerillas debe ser la siguiente. Como 37 no es múltiplo de siete, en la primera jugada coger dos cerillas para que le queden 35, que es múltiplo de siete y en las siguientes, cuando B coja un número x de fósforos (x entre 1 y seis), A tomará 7- x. De forma parecida a como se hace en la tabla siguiente:
Si disponemos de un número N de cerillas y los jugadores A y B optan por coger alternativamente, un número x de fósforos (x entre 1 y n) una. Ocurre lo siguiente:
- Si N es múltiplo de n +1, el jugador B que juega en segundo lugar, tiene una estrategia ganadora y es mantener la pauta de que si A toma x cerrillas B cogerá n – x +1 de esta forma B cogerá la última cerilla y ganará el juego.
- Si N no es múltiplo de n +1 el juego, el jugador A, que juega en primer lugar, tiene una estrategia ganadora y es dejarle a B, tras la primera jugada, un múltiplo de n + 1 Luego B cogerá x cerillas y A cogerá n – x +1 de esta forma A cogerá la última cerilla y ganará el juego.
Con palillos y cerillas hay muchos huegos interesantes de cara estudiar estrategias ganadoras, por ejemplo, imaginemos que dos jugadores A y B están frente a dos montones de cerillas que retiran alternativamente una o más piezas de un solo montón y que gana el que toma la última cerilla. Se pueden dar dos casos.
- Si los dos montones tienen el mismo número de cerillas, B, que juega en segundo lugar, dispone de una estrategia ganadora sencilla que consiste en mantener la igualdad de ambos montones. Esto es, si A retira n cerillas del montón uno B retira n cerillas del segundo montón. Esta estrategia le asegura a B el último movimiento ganador.
- Si los dos montones tienen N y N+1 cerillas, entonces A, que juega en primer lugar, podría coger una cerilla del montón mayor de manera que los dos montones quedaran iguales, convertirlo en el juego con montones iguales y B debe perder

