
Una de las características más destacables de la pintura medieval era el tamaño diferente de las personas y de los objetos representados en el cuadro para indicar proximidad o lejanía respecto al observador o destacar la importancia de un objeto o una persona en la escena representada. En muchas ocasiones los tamaños de las diferentes figuras representadas no guardaban proporción con los objetos de su alrededor.
Los artistas medievales se regían, habitualmente, por un criterio diferente a la perspectiva y era que el tamaño de los objetos de un cuadro venía dado por la mayor o menor importancia que el pintor concedía a cada uno, con independencia de su situación espacial. Y rellenaban el cuadro con un conjunto de figuras sin conceder excesiva importancia al paisaje que era simplemente de relleno. Esto puede apreciarse en la tabla del retablo del Maestro de Torralba (principios del s. XV) de la Iglesia de San Félix de Torralba de Ribota (Zaragoza) en la que aparece San Félix predicando.
Frente a los pintores medievales, los pintores renacentistas pretendían representar fielmente el mundo tridimensional que les rodeaba en las dos dimensiones de un lienzo. Para ello se sirvieron de la perspectiva. L. Battista Alberti (1404-1472) lo describía así en los Tres libros de la pintura (1435):
Para pintar una superficie, lo primero hago un cuadro o rectángulo del tamaño que me parece, el cual me sirve como una ventana abierta, por la que se ha de ver la historia que voy a expresar, y allí determino la estatura de las figuras que he de poner, cuya longitud la divido en tres partes. Estas partes para mí son proporcionales a aquella medida que comúnmente llaman braza (48 cm. aproximadamente); pues según se advierte en la proporción del hombre, su regular longitud es de tres brazas. Con esta medida divido la línea que sirve de base al rectángulo, y anoto las veces que entra en ella.
Hecho esto, señalo un punto adonde se ha de dirigir principalmente la vista, dentro del rectángulo, […] le llamo punto del centro. Este punto se colocará en paraje conveniente, no más alto que la altura que se señala a las figuras en aquel cuadro. Señalado el punto del centro, tiro rectas desde todas las divisiones de la línea de la base a él, las cuales me demuestran el modo con que van disminuyendo las cantidades.
El procedimiento se ilustra en el siguiente grabado de A. Durero (1471-1528)

Los pintores partían de la interpretación de una propiedad fundamental de la visión monocular, era que los rayos de luz partían de los objetos hasta nuestro ojo y el artista lo que debía pintar eran los puntos de intersección con el plano del lienzo de los rayos que partían de los objetos hasta nuestro ojo. El lienzo se suponía transparente. Con este procedimiento para que cualquier observador de su pintura pudiera recibir la misma percepción de la escena tridimensional que él.
Pero como el lienzo del artista no era transparente, la tarea de plasmar con exactitud la proyección deseada planteaba problemas. Existe además otra dificultad añadida y era que nuestra visión es binocular, cuestión que los pintores trataron de resolver jugando con las sombras y la variaciones en la intensidad de la luz.
El éxito de la perspectiva en la pintura fue colosal e hicieron uso magistral del técnica grandes pintores como L. da Vinci (1452-1519) en el fresco de la Santa Cena de Santa Maria delle Grazie de Milán, Rafael de Sanzio (1483-1520) en La escuela de Atenas, en el palacio Apostólico de la ciudad del Vaticano o Pietro Perugino (1448- 1523),en el fresco de la Capilla Sixtina Entrega de llaves a San Pedro, tuvieron que representar las escenas de manera más realista haciendo uso de los principios de proyección y sección.
Alberti planteó una cuestión básica desde el punto de vista matemático: se preguntó lo que debían tener en común el objeto original y cualquiera de sus secciones de los rayos que partían de los objetos al ojo del artista por un plano arbitrariamente elegido. Era obvio que ni las distancias ni los ángulos se conservan al proyectar y seccionar una figura. Tratar de dar una respuesta a la pregunta de Alberti condujo, en el siglo XV, a la creación de una teoría de la Perspectiva Geométrica.
La composición de un cuadro se realizaba en el plano pictórico y se creaba por la intersección de los rayos de la pirámide visual con un plano, que era el lienzo. El plano podía tener cualquier inclinación y la representación podía ser diferente, pero, en todas ellas, se reconocía el mismo objeto real y la pregunta de Alberti se puede formular del siguiente modo ¿qué propiedades comparten las distintas secciones de la pirámide visual para que produzcan la misma impresión sobre el ojo?
Aunque no se conservaban ni ángulos ni distancias la recta seguía siendo recta en cada sección. En cada sección se mantenían los elementos fundamentales que eran los de punto y recta y la relación de pertenencia (o incidencia). La teoría de la Perspectiva Geométrica fueron los comienzos de la Geometría Proyectiva y para estudiar las propiedades invariantes por proyección y sección se utilizó la Geometría de Euclides (no se conocía otra en el siglo XVI).
El invariante numérico que interviene para cuatro puntos A,B,C,D es su razón doble, que se escribe (A,B,C,D) = (CA/CB):(DA/DB), ya que cuatro puntos alineados A,B,C,D se pueden transformar en otros cuatro A’,B’,C’,D’ si la razón doble de los primeros es la misma que la de los segundos. Es decir si (A,B,C,D)=(A’,B’,C’,D’)
Los puntos correspondientes por proyección-sección no conservan la razón simple:
(ABC) ≠(A’B’C’) , ya que
![]()
solamente si CA y C’A’ son paralelas
Sin embargo, los puntos correspondientes por proyección-sección, aunque no conservan la razón simple, conservan la razón doble como mostrams a continuación:
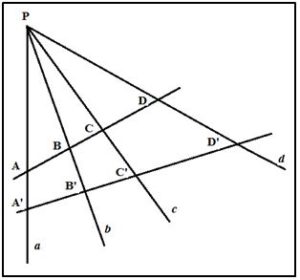
Sea la radiación formada por las cuatro rectas a, b, c, d y las rectas transversales AD y A’D’, como se observa en la figura. Llamemos Ar (APC) al área del triángulo APC y (ac) al ángulo formado por las rectas a y c, entonces tenemos:
- Ar (APC) = (1/2) PA·PC sen (ac) = AC·h
- Ar (BPC) = (1/2) PB·PC sen (bc) = AB·h
Dividiendo se obtiene:
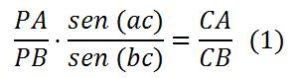
además
- Ar (APD) = (1/2) PA·PD sen (ad) = AD·h
- Ar (BPD) = (1/2) PB·PD sen (bd) = BD·h
Dividiendo:
![]()
Finalmente, dividiendo (1) entre (2), se obtiene:
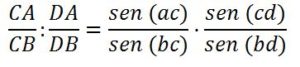
Como la razón doble depende del seno se los ángulos que subtienden las rectas de la radiación, será la misma para los puntos A’,B’,C’,D’ luego (A,B,C,D)=(A’,B’,C’,D’) y, por lo tanto, se conserva la razón doble.




