Cuando en la actualidad hablamos de números nos imagínanos la sucesión de los números que empleamos para contar, es decir, una cadena indefinida, por un lado, asciende hasta los más grandes, y, por otro, desciende hasta lo más pequeño. Los griegos tenían esta representación esta idea, pero si que destacaban unas características particulares que ahora, en muchos casos, son curiosidades, que interesan a los matemáticos y que ahora, muchas de ellas están en desuso. Era como descubrir y describir diferentes clases de números como si se tratara de diferentes especies biológicas.
Unas de estas características particulares dividían el conjunto de los números (enteros positivos) en dos partes, como como sucedía con la división en números pares e impares o la partición en números primos y compuestos. Otras características eran de carácter geométrico, que ponían el acento en la figura geométrica que se podía formar con las unidades que expresaban y aparecían los números triangulares (si sus unidades de podían disponer en forma de triángulo equilátero), cuadrados (si sus unidades de podían disponer en forma de cuadrado), y, con el mismo criterio, números pentagonales, hexagonales, etc. Por la misma razón, había números cubos o piramidales.
Estas clasificaciones eran más caprichosas que las anteriores, porque algunas clases tenían elementos comunes; por ejemplo, el 64 es cuadrado y cubo a la vez y el 36 es el octavo número triangular y, además, es cuadrado. Otras características se debían a sus propiedades por descomposición entre ellos como múltiplos y divisores; o relaciones más complejas como entre parejas de números por sus divisores como los números amigos o permitían identificar una propiedad individual de cada número, es el caso de los números perfectos, que estudiaremos a continuación. Los números perfectos se definen de la siguiente forma.
DEFINICIÓN. – Se llama número perfecto al número natural que es igual a la suma de sus divisores propios positivos. (No se cuenta como divisor el propio número)
EJEMPLO: El 6 es un número perfecto, ya que tiene por divisores propios 1, 2 y 3 y su suma 1 + 2 + 3 = 6.
OBSERVACIÓN:
Si la suma de los divisores propios de un número natural n es mayor que n, el número se llama abundante. Por ejemplo 48 es abundante (1+ 2 + 3+ 6 + 8+ 12 + 16+ 24 = 72 > 48).
Si la suma de los divisores propios de un número natural n es menor que n, el número se llama deficiente. Por ejemplo 27 es deficiente (1 + 3 + 9 = 13 < 27)
A continuación, se dan los siguientes resultados sobre números perfectos:
PROPOSICIÓN 1.- Ningún número primo es un número perfecto
Dem: Es evidente, el único divisor propio de un número primo es la unidad.
PROPOSICIÓN 2.- Ninguna potencia de un número primo es un número perfecto
Dem : Sea N = pa, y p un número primo y a entero positivo. Para que N sea número perfecto la suma de sus divisores propios 1, p, p2, p3, …. pa-1 (pa no entra) debe cumplir:
![]()
Como p ≥ 1 se tiene que la suma de sus divisores será:
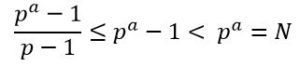
Por lo tanto, la suma de sus divisores propios será menos que N y N = pa no será un número perfecto, sino un número deficiente.
A continuación, vamos a probar la propiedad más importante de números perfectos. Ya que proporciona una fórmula para calcular números perfectos.
Calcular p para que N = p·2n sea un número perfecto.
Todos los divisores de N (incluido el propio N) serán los sumandos del producto:
(1 + p) (1 + 2 + 22+ 23+ …+2n )
Por lo tanto, ese producto debe ser igual a 2N
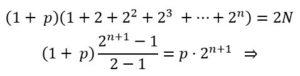
⇒ (1 + p) (2n+1-1) = p 2n+1 ⇒ 2n+1-1 + p2n+1– p = p2n+1 ⇒
⇒ 2n+1– 1 – p = 0 ⇒ 2n+1– 1 – p = 0 ⇒ p = 2n+1– 1
Lo que nos lleva a la siguiente proposición:
PROPOSICIÓN 3.- Si p es un número primo de la forma p = 2n+1– 1, los números de la forma N = p 2n son número perfectos,
Es decir, los números de la forma: N = 2n (2n+1– 1) son números perfectos
Libro IX de los Elementos, Euclides expresa así el resultado en su proposición 36,
Proposición 36. Si tantos números como se quiera a partir de una unidad se disponen en proporción duplicada hasta que su suma total resulte un número primo y el total multiplicado por el último produce algún número, el producto será un número perfecto
OBSERVACIÓN:
- El número se 6 tiene divisores 1, 2, 3 y cumple que (1/1) + (1/2) + (1/3) + (1/6) = 2
- El número se 28 tiene divisores 1, 2, 4, 7,14, 28 y cumple que (1/1) + (1/2) + (1/4) + (1/7) + (1/14) + (1/28) = 2
Con las observaciones anteriores demostrar la siguiente proposición
PROPOSICIÓN 4.- La suma de los inversos de los divisores de un número perfecto N (incluido el inverso del propio N) es 2
Libro IX de los Elementos, Euclides laexpresa así en su proposición 36,
Proposición 36. Si tantos números como se quiera a partir de una unidad se disponen en proporción duplicada hasta que su suma total resulte un número primo y el total multiplicado por el último produce algún número, el producto será un número perfecto