JUEGOS DE PESAS, PESADAS Y SISTEMAS DE NUMERACIÓN

 

El sistema de numeración binario de base dos es posicional y utiliza solamente las cifras 0 y 1.  En este sistema de numeración cualquier número entero positivo puede representarse de manera única como suma de potencias distintas de dos, entonces ese nnúmero está expresado en base dos .

Con un juego de pesas de 1, 2, 4, 8, 16, 32,… podemos pesar cualquier objeto cualquiera que sea su peso. Por ejemplo: unos objetos de pesos de 3, 13, 23 y 55 gramos se pueden equilibrar con las pesas potencias de dos que se indican a continuación:

                                       3 = 2 + 1,         13 = 8+ 4 +1,         23 =  16 +4 +2 +1,         55= 32 +16 +4 +2+1

Para saber las pesas que se necesitan para pesar un objeto con pesas que sean potencias de dos,  basta con expresar el peso del objeto como suma de potencias de dos, lo que equivale a expresar ese número en base dos. Así:

                                                      55 = 32 + 16 + 4 + 2 + 1 = 2⁵ + 2⁴ + 2² + 1 = 110101₂

Para hacer la conversión de un número n expresado en base decimal al sistema  binario se procede del siguiente modo: se divide el número expresado en base diez entre dos,  se anota el resto y se sigue dividiendo cada cociente hasta llegar a cociente uno.  Para escribir el número n binario tomaremos el último cociente (que siempre será 1) y todos los restos de las divisiones de abajo arriba, orden ascendente, como se indica  para el número 42:

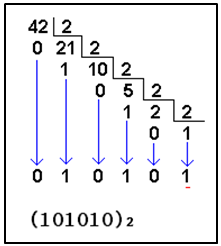
                     42 = 1·2⁵ + 0·2⁴+ 1·2³ +  0·2² + 1·2¹ + 0 ·2⁰ =

                                   = 32 + 8 + 2 = (101010)₂

Como hemos señalado al principio las únicas cifras necesaria para expresar cualquier en sistema binario número son 0 y 1, Ya que los restos al dividir por dos sólo pueden se ceros y unos.

Como consecuencia si queremos pesar un objeto de un peso cualquiera,  N ,con un único juego de pesas   de la balanza de 1, 2, 4, 8, 16, 32,… gramos, lo que debemos hacer es expresar N en base dos y se seleccionan la pesas que se corresponden con los lugares que tienen uno. Si queremos pesar un peso de 100 gramos

                                                            100 = 1·2⁶ + 1·2⁵ + 0·2⁴ +  1·2³ + 0·2² +  0·2¹ +0·2⁰ =

                                                             = 1·64 + 1·32 + 1·8 = 1101000₂.

Tomaremos una pesa de 64, otra de 32 y otra de 8 gramos.

Por lo tanto, con una balanza de dos platillos y un juego de pesas de 1, 2, 4, 8 , 16,… gramos se puede pesar cualquier objeto con la precisión de un gramo, colocando el cuerpo que deseamos pesar en un platillo y las pesas necesarias en el otro. Ya que cualquier peso que nos den se puede expresar como suma de potencias distintas de dos.

Sin embargo, con una balanza y un único juego de pesas de 1, 3, 9, 27, 81, … gramos no se puede pesar cualquier objeto colocando el cuerpo que deseamos pesar en un platillo y las pesas necesarias en el otro. Ya, por ejemplo, para pesar un objeto de 26 gramos  necesitamos dos pesas de un gramo, dos de tres gramos y otras dos de nueve gramos.  Ya que:

             26 = 2·9+ 2·3 + 2·1 = 2·3² + 2·3¹ + 1·3⁰ = (222)₃

Además, el teorema fundamental de la numeración nos asegura que, dada una base B > 1, todo número N se puede descomponer de  forma única como:

                                                             N= a + b·B + c·B² + d·B³ +····+ l·B^k

Siendo los números (cifras) a, b, c, d,.., l  menores que la base B.  El número N se escribe en la forma  (l k … c b a)_B.

Si tenemos un un único juego de pesas de 1, 3, 9, 27, 81, … no podermos pesar cualquier objeto colocando las pesas en un platillo de la balanza.  Pero, sin embargo, si que podemos pesar cualquier objeto si se nos permite colocar pesas en ambos platillos de la balanza para equilibrar:

Supongamos que el cuerpo pesa P gramos y consideramos que el número P es entero.  El número P se puede representar en base tres,

                                                                   P  = a·3ⁿ +  b·3 ^n-1 +… +  k·3 + l,

Donde los coeficientes a, b, c, …, k, l   toman los valores 0, 1 ó 2.

Para hacer la conversión de un número expresado en base decimal al sistema  en base tres, se divide el número entre tres,  se anota el resto (que será 0, 1 o 2) y se sigue dividiendo cada cociente hasta llegar a cociente uno o dos.  Para escribir el número en base tres cogeremos tomaremos el último cociente (que  será 1 o 2)  y a continuación todos los restos de las divisiones de abajo arriba, orden ascendente.

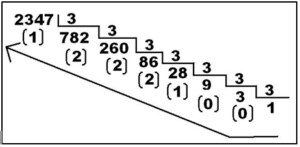
2347 = (10012221)₃ = 1·3⁷ + 0·3⁶ + 0·3⁵ + 1·3⁴ + 2·3³ + 2·3² + 2·3¹ + 1·3⁰

En el caso de sistema ternario las únicas cifras que se necesitan para escribir cualquier número son 0, 1 y 2. Ya que los restos al dividir por tres sólo pueden se ceros y unos y doses.

Pero podemos hacer una variación en el sistema ternario, empleando las cifras 0, 1 y -1 en lugar de 0, 1 y 2. Para obtener esta representación, convertimos el número P escrito en el sistema decimal al sistema ternario, pero, para evitar los doses que puedan aparecer como restos en las divisiones sucesivas, cada vez que al dividir entre tres obtengamos resto 2, aumentaremos el cociente en una unidad y escribiremos el resto en la forma de -1. (es decir, calculamos el cociente por exceso y el resto por defecto será negativo. Así, obtendremos una nueva  representación del número

                                                                             P  = a’·3ⁿ +  b’·3 ^n-1 +… + k’·3 + l’ ,

Donde cada coeficiente a’, b’, c’,…, k’, l’  es igual a 0, 1 ó -1.

Por ejemplo, para pesar un objeto de peso P = 100 gramos,  expresaremos el número en base tres:

                                                                     100 = 1·3⁴ +0·3³+ 2·3²+ 0·3¹+ 1 = (10201)₃ 

se necesitarán: una pesa de 81gramos, dos pesas 9 gramos  y un se un gramo con lo que las pesadas no podrán realizarse con un solo  juego de pesas colocando el objeto en un platillo y las pesas en el otro.

Sin embargo, si, cuando aparece el resto 2, calculamos el cociente por exceso, el resto será -1, que representará la pesa que debemos colocar en el platillo en el que esté ubicado el cuerpo que deseamos pesar.

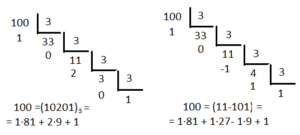
Aplicando este procedimiento, como

               100 = (1 1 -1 0 1)₃ = 3⁴ + 3³ – 3² + 1.

Luego para pesar un objeto de 100 gramos colocaremos el objeto y una pesa de 9 gramos en el primer platillo de la balanza y las pesas de 1 gramo, la de 27 y la de 81 gramos en el segundo, con lo que en cada platillo hay 109 gramos y la balanza estará equilibrada.