La media aritmética de dos o más números es la media que utilizamos con mayor frecuencia. Cuando un alumno recibe tres calificaciones como 4, 5 y 9 sabe que la nota que le corresponde es un 6 que es la media aritmética de sus calificaciones. Este principio, tan bien aprendido y tantas veces utilizado, hace que, en ocasiones, olvidemos que hay otros tipos de media; una de ellas es la media armónica que aparece cuestiones como la siguiente:
Un motorista realiza la mitad de un recorrido de 2r km a una velocidad d e 100 km/h y la otra mitad a 70 km/h ¿Cuál será la velocidad media con la que ha hecho el recorrido completo?
La respuesta inmediata es que la velocidad media es la media aritmética de las velocidades y decir que la moto ha llevado una velocidad media de 85 km/h, pero no es así, puesto que la velocidad media no es la media aritmética de las velocidades, sino que es la velocidad constante que debería llevar otra moto para hacer el recorrido en el mismo tiempo.
El tiempo empleado en recirrer 2r km por el motorista será:
y la velocidad media:
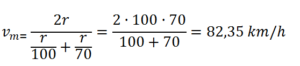
En este caso (recorren espacios iguales con la misma velocidad) la velocidad media de dos velocidades v y v’ será:
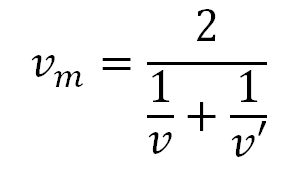
Lo que significa que velocidad media de la moto es la media armónica de las velocidades v y v’
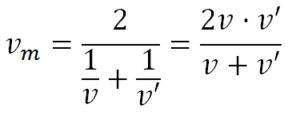
Con esta idea se define la media armónica, H, de N números como el recíproco de la media aritmética de los recíprocos de dichos números:
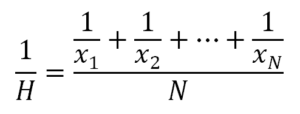
En música se emplean, tanto la media aritmética como la media armónica para determinar las otras notas musicales, dentro de las escalas.
La media aritmética de las frecuencias de la nota DO de la cuarta escala musical y la nota DO de la escala siguiente, son 262 Hz y 523 Hz respectivamente y representan un Do y su octava. La nota que tiene de frecuencia la media aritmética de ambas, 391,5 Hz, será la quinta de Do, esto es, un Sol
La media armónica de la frecuencia de ambas notas nos da una nota de frecuencia 349 Hz, una nota Fa, que es la cuarta de Do
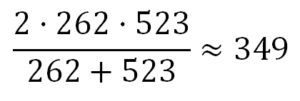
Esta es una propiedad que se usó para la afinación musical por quintas en la afinación Pitagórica. Si una nota tiene una frecuencia f su octava más aguda tendrá una frecuencia f ‘ =2·f . La media aritmética de la frecuencia de ambas notas será:
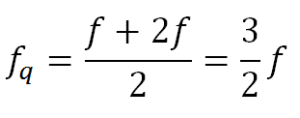y la media armónica
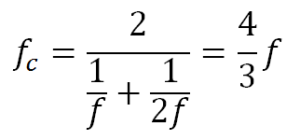
Estos resultados concuerdan con los descubrimientos musicales de Pitágoras en el siglo VI a. C. que podemos resumir diciendo que si de una cuerda de longitud 2u dejamos vibrar la mitad (una longitud u) suena una octava de la nota principal. Si vibra una longitud de 3/2 suena una quinta de la nota y si suena 4/3 una cuarta, que son los sonidos consonantes que sirvieron de base a la afinación musical hasta el siglo XVIII.
