Cuando el hombre estudia la naturaleza física se encuentra con la materia y su comportamiento a lo largo del tiempo. Puede descubrir situaciones que considere desordenadas, imprevisibles e incluso fortuitas, pero, a veces, descubre procesos regulares y entonces emprende la labor de comprender el fenómeno y tratar de descubrir sus causas o describir su comportamiento.
Las ciencias físicas hacen una descripción de la Naturaleza en lenguaje matemático. Describiendo los fenómenos naturales mediante fórmulas matemáticas podemos preguntarnos de si esas leyes físicas son creaciones humanas que describen de forma más o menos precisa el proceder de los fenómenos o, por el contrario, si las leyes se encuentran en la naturaleza esperando ser detectadas de forma parecida a como se descubrieron las ondas electromagnéticas, la emisión radiactiva o la descomposición de la luz.
Comenzaremos analizando dos ejemplos: el primero es el Teorema de Pitágoras que es una ley que cumple el espacio en que nos movemos. Lo conocían los antiguos babilonios y los egipcios y, además, siempre que observemos un triángulo rectángulo se verificará. Y podemos pensar que, aunque lo formuló Pitágoras (569-475 a.C.), descubrir esa relación era cuestión de tiempo y muchos consideran que no es invención humana, sino que era algo que estaba impreso en la naturaleza y se descubrió, como se descubre un mineral precioso entre la ganga.
Otra ley elemental de la naturaleza es el valor de la aceleración gravitatoria y la ley de la velocidad con que de un cuerpo en caída libre alcanza el suelo dejado caer desde una altura h:
Esta ley fue descubierta por Galileo (1564-1642) estudiando la caída de los cuerpos por planos inclinados y era, aparentemente, más complicada de descubrir que el teorema de Pitágoras, pero ambas fórmulas son relaciones numéricas entre magnitudes medibles y aún se podría decir que son leyes que se pueden descubrir porque están ahí.
Esta visión sugiere la idea de que una ley matemática de la Naturaleza existe antes de que alguien la formule. Es decir, que leyes están agazapadas y escondidas en la Naturaleza modo que, aunque no conociéramos el teorema de Pitágoras sería una relación que se cumple en nuestro espacio ordinario y permanecería ahí esperando ser descubierta. Lo mismo podríamos pensar de leyes tales como la Ley de Gravitación.
Estas reflexiones participan de una visión platónica del mundo que sugiere que las leyes científicas, como las ideas platónicas, tienen vida entre nosotros, están en la naturaleza y se descubren como se alcanzan las ideas en el Mito de la caverna de Platón .
El pensamiento neoplatónico del siglo XVII mantenía que las matemáticas eran la estructura que vertebraba el universo, en palabras de Galileo en Il Saggiatore (1623):
La filosofía [natural] está escrita en ese grandioso libro que tenemos abierto ante los ojos, (el universo), pero ese libro no se puede comprender si antes no se ha aprendido la lengua,…. Está escrito en lenguaje matemático y sus caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible entender ni una palabra; sin ellos es como girar vanamente en un oscuro laberinto.
Galileo apunta la idea de que las matemáticas aportan el lenguaje único y universal con el que se pueden describir y exponer las leyes más profundas de la Naturaleza, leyes que transcienden la capacidad de observación humana. De hecho, las leyes matemáticas de la Naturaleza nos llevan a hacer descubrimientos nuevos y, en ocasiones, aplicarlas a cuestiones no previstas inicialmente. Cuando I. Newton (1642-1727) formuló la Ley de Gravitación Universal pretendía explicar las leyes del movimiento de los planetas, pero la Ley le permitió explicar la causa de las mareas oceánicas, la forma de la Tierra, e incluso que a partir de ella el astrónomo francés J.J. Le Verrier (1811-1877) predijera la existencia del planeta Neptuno en 1845. Las leyes matemáticas nos permiten descubrir cosas que están alejadas de la observación ordinaria.
Casi todos los científicos opinan que las matemáticas con las que se interpreta el libro de la naturaleza al que aludía Galileo son una creación de la mente humana. De hecho, las matemáticas a lo largo de la historia se han ocupado de temas con grado de abstracción cada vez mayor y, sobre todo, desde comienzos del siglo XIX. En ese momento aparecieron las geometrías no Euclidianas, surgió la noción de espacio curvo y emergiern otros espacios viables, las matemáticas se alejaron de la intuición y su validez no se podía justificar por estar de acuerdo con la observación. En realidad se abrieron nuevos modelos para interpretar la estructura espacio en el que se producían los fenómenos naturales.
R. Hersh, en su libro ¿Qué son las matemáticas realmente? (1997) mantenía que las matemáticas eran una creación humana parecida a la música, la poesía o las leyes del derecho. Frente a los que decían que las leyes matemáticas eran una invención libre de la razón, los neoplatónicos argumentaban que si las matemáticas fueran un creación mental resultaría difícil de explicar el hecho de se ajustatan tan maravillosamente al comportamiento de la Naturaleza y se pudieran hacer con ellas predicciones sobre el comportamiento de los fenómenos con asombrosos niveles de precisión.
P. Dirac (1902-1984) describió la situación diciendo que los matemáticos jugaban a un juego en el que ellos mismos imponían sus reglas, mientras que a los físicos las reglas del juego les venían dadas por la Naturaleza. Pero lo asombroso era que las reglas de juego que eran interesantes para los matemáticos eran las que había elegido la naturaleza para su funcionamiento.
Si aceptamos que las matemáticas son un invento de la mente humana que se adapta al funcionamiento de la Naturaleza nos podemos preguntar de dónde salen las Leyes Físicas. Parece evidente que salen de la observación de regularidades y comportamientos análogos que observamos en la Naturaleza. Los astros recorren sus órbitas sin cesar con un comportamiento fijo, la caída de los graves sigue la vertical y tiene aceleración constante, las leyes de Mendel señalan comportamientos estadísticos regulares en la en la herencia genética, etc.
El descubrimiento de comportamientos regulares en la Naturaleza es fundamental para la ciencia. Las regularidades observadas no eran invenciones de la mente humana. Esa hipótesis es fundamental para hacer ciencia ya que cuando el hombre observa estas regularidades aventura, hipótesis y busca relaciones matemáticas entre los fenómenos observados en la Naturaleza. Las leyes son creaciones de la mente humana; pero son un intento de expresar, aunque sea de forma aproximada, el comportamiento de la Naturaleza.
Esa es la labor del científico: descubrir leyes que describan lo mejor posible el comportamiento de la Naturaleza. Pero una vez formuladas las leyes se suele dar un salto a un nivel superior. Las leyes matemáticas de la Naturaleza que únicamente describen cómo se comporta un fenómeno pasan a considerarse como leyes de ordena y manda y, en la literatura cientifica aparecen expresiones como: los planetas obedecen las Ley de Gravitación Universal o el comportamiento del Universo está sometido a las Leyes de la Termodinámica. Como si una ley ajena al planeta lo obligara a llevar un movimiento regular o como si el Universo que surgió del Big-Bang necesitara unas leyes que señalaran los límites de su evolución.
Dejaremos este tema más filosófico y pondremos un ejemplo que pone de manifiesto el maridaje entre las matemáticas puras y las primeras intuiciones físicas sobre la Relatividad General de A. Einstein (1879-1955). Einstein partía de la intuición de que si nos encontramos dentro en una cabina cerrada y realizamos cualquier experimento dentro de ella no podremos determinar si estamos en reposo sobre la superficie de la Tierra (sometidos a una campo gravitatorio de aceleración g) o si la cabina lleva un movimiento acelerado (con aceleración g) a través del espacio a mucha distancia de cualquier cuerpo.
Pensó que un rayo de luz que se emitiera horizontalmente en la cabina sería desviado en el sentido de la aceleración de misma y que, por tanto, los rayos de luz que se propaguen a través de cualquier campo gravitatorio serían desviados en la dirección y sentido de la fuerza gravitatoria.
Einstein comprendió que no podía utilizar Euclidiana en un mundo en el que la luz no se propagara en línea recta cuando pasaba cerca de un cuerpo de gran masa y vio la necesidad de emplear la geometría de Riemann como soporte de la teoría gravitación de su física.
Para dar soporte matemático a su teoría y a instancias de M. Grossmann (1878-1936), matemático y antiguo compañero de Einstein, utilizó el Cálculo Tensorial desarrollado, apenas un par de décadas antes por G. Ricci-Curbastro (1853-1925) y su discípulo T. Levi-Civita (1873-1941). De ese modo, una teoría matemática, creada con libertad y alejada de la intuición física sirvió para dar forma a la Teoría General de la Relatividad con la siguiente fórmula:
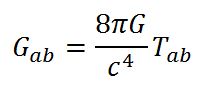en la cual Gab es el tensor de Einstein, que depende de la métrica del espacio-tiempo y de sus primeras y segundas derivadas respecto a las coordenadas. Este tensor representa la las maneras de moverse un punto en el espacio-tiempo. El término (8πG)/c4 es una constante de proporcionalidad. Y Tab es el tensor de energía, que contiene la información sobre el tipo de energías (y masas E = mc2) del espacio-tiempo y de su propagación.
Esa bonita fórmula, tan compacta y de apariencia sencilla, sintetiza la expresión de diez ecuaciones no lineales en derivadas parciales de no fácil solución, pero expresa la profunda relación entre la pura geometría del espacio-tiempo (Gab) y la realidad físca (Tab).
Esta fórmula es el ejemplo tangible de la hermosa afirmación de E. Wigner (1902-1995) que dice: El milagro de la adecuación del lenguaje de las matemáticas para formular las leyes de la física es un regalo maravilloso que ni entendemos ni merecemos.
