
Los científicos han considerado a las Matemáticas como un lenguaje neutro liberado de opiniones y de juicios subjetivos con el que se podían expresar, tanto los datos experimentales como los resultados científicos extraídos de ellos. No entraré en especulaciones sobre que si las Matemáticas son creación humana o sobre si son algo como un mineral que podamos encontrar en la naturaleza y sobre cuya aparición debía hacerse antes o después, pero dentro de las Matemáticas están contenidas muchas teorías diferentes y la elección de una u otra para sistematizar y explicar los fenómenos físicos está cargada de subjetividades, una de las cuales es la de elegir la propia teoría matemática por la belleza con la que se pueden organizar con ella los fenómenos observados y dar explicación de los mismos.
Voy a tratar de describir unas ideas sugerentes que expone la doctora S. Hossenfelder en su libro Perdidos en las Matemáticas para mostrar cómo la belleza de las Matemáticas actúa como principio metafísico de la ciencia (utilizando el término metafísico, como un criterio extra-científico que influye en la elaboración de las teorías físicas). Es cierto que, desde el nacimiento de la Ciencia Moderna, las Matemáticas y la Física han ido siempre de la mano, pero, mientras que las Matemáticas son una creación libre del espíritu humano a las que se les exige únicamente coherencia lógica, las teorías físicas tienen una exigencia más y es que, además de ser coherentes desde el punto de vista lógico, tienen que adaptarse a la observación, lo que significa que una teoría físico-matemática tiene que describir la evolución de los acontecimientos y sus predicciones no pueden contradecir los datos observados.
Entender las matemáticas no es la tarea más difícil que tiene el físico. Es cierto que tiene la dificultad de que las teorías matemáticas que se utilizan tienen ellas mismas diferentes lenguajes y aplicar una teoría matemática para actualizar una teoría anterior necesita, casi siempre, una labor de traducción. Newton (1643-1727) la escribió su mecánica en lenguaje geométrico, L. Euler (177-1783) y J.L. Lagrange (1736-1813) utilizaron Cálculo Diferencial para describirla. C Maxwell (1831-1879) empleó los cuaterniones de W. R. Hamilton (185-1865) para su teoría electromagnética y luego fue traducida al cálculo vectorial, etc. Pero la dificultad esencial para elegir una teoría matemática está en saber cuál es adecuada para describir sin contradicción alguna los hechos observados. Pero para demostrar la coherencia de una nueva teoría física con la anterior es necesario analizar la concordancia de la misma con tal cúmulo de datos observacionales, que no es factible realizar los cálculos uno a uno. Entonces el físico teórico procede de la siguiente forma:
Primero demostramos que la nueva teoría coincide con la antigua ya confirmada, para medir así su precisión, reproduciendo los logros de la teoría anterior. De ese modo que sólo tenemos que incorporar los cálculos relativos a las novedades que la nueva teoría pueda explicar (S. Hossenfelder Perdidos en la Matemática p.22)
El problema reside en demostrar que una teoría física nueva reproduce los logros de la otra teoría física anterior, pero la cuestión no es fácil. Pensemos en la Teoría General de la Relatividad de A. Einstein (1879-1955), que era la nueva teoría que reproducía las predicciones de la Teoría Gravitación Universal de Newton. Einstein dedicó mucho esfuerzo y mucho tiempo, de 1909 a 1915, para probar que su Teoría reproducía los éxitos de la Mecánica Newtoniana, dentro de una teoría que admitiera, además, el principio de equivalencia. Einstein no sabía cómo encajar la interacción gravitatoria de Newton en su Teoría; las matemáticas que utilizaba eran válidas, pero no cuadraban con el mundo real, finalmente, con el Cálculo Tensorial de G. Ricci Cubastro (1853-1925) y T. Levi Civitá (1873-1941) y encontró la matemática adecuada con la que encajar los datos del rompecabezas de la Teoría General de la Relatividad, que lo llevó a identificar el potencial gravitatorio newtoniano como una manifestación de la curvatura del espacio tiempo producida por la distribución de masa. Ley dada por la siguiente ecuación:
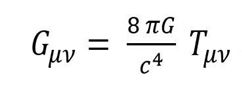
La ecuación de Einstein describe como el contenido de energía y materia, codificado en el tensor de energía-momento, Tμν, determina localmente la curvatura del espacio tiempo, codificada en el tensor de Einstein Gμν.
Análogamente a lo que sucedió en el caso de la Relatividad General, para elaborar una teoría física hay que buscar una teoría matemática que aplicada a los datos experimentales permita reproducir los resultados de la teoría anterior y que dé cuenta de las observaciones realizadas. Pero es evidente que cuantas más observaciones haya que incluir la nueva teoría, más compleja y más difícil será probar las mejoras planteadas por la teoría: S. Hossenfelder señala, para poner de manifiesto el factor extracientífico en la elección de las teorías matemáticas, hechos tan llamativos y sugerentes como los siguientes:
La existencia del neutrino fue propuesta por W. Pauli (1900-1958) en 1930. La partícula no debía tener carga eléctrica, por eso E. Fermi (1901-1954) lo denominó con la palabra italiana neutrino y tuvieron que pasar más de veinticinco años hasta que, en 1956, los físicos F. Reines (1918-1998) y C.L. Cowan (1919-1974) encontraron evidencias de reacciones de neutrino que se originaban en un reactor. Igualmente pasaron alrededor de cincuenta años para confirmar la existencia del bosón de Higgs, anunciado por Peter Higgs (1929-) en 1964 y confirmada su existencia gracias al LHC (Gran Colisionador de Hadrones) por Joe Incandela (1956-) y Fabiola Gianotti (1960-) en 2012.
También pasaron cien años para detectar directamente las ondas gravitacionales, que habían sido anunciadas en 1915 por A. Einstein en su Teoría de la Relatividad General y fueron detectadas el 14 de septiembre de 2015 por los físicos americanos Barry Barish (1936-), Rainer Weiss (1932-) y Kip Thorne (194-), que recibieron el premio Nobel en 2017.
Con estas constataciones, S. Hossenfelder destaca que la ciencia actual realiza unas predicciones cuya comprobación encierra tal complejidad que el tiempo necesario para probarlas o refutarlas experimentalmente es muy largo. Es más, el tiempo necesario para probar una ley fundamental de la naturaleza puede ser más largo que toda la carrera de un científico, sin mencionar que se precisan aparatos costosos y escasos como el LHC.
El largo periodo de tiempo que media entre una predicción teórica de una partícula o de un fenómeno físico y su comprobación experimental hace que muchos científicos trabajen con teorías no probadas, que probablemente serán verdaderas, pero, como no están constatadas se mueven en un mundo hipotético, que hace que una o varias generaciones de científicos investiguen con las dudas de si será validez física de sus teorías. Esta situación provoca que muchos físicos opten por elegir teorías matemáticas diferentes para explicar los hechos. Y los científicos, para elegir la teoría matemática adecuada, recurren a criterios que no se reducen a la adecuación empírica y, entre esos criterios, está el atractivo estético de las teorías matemáticas. Y se suelen plantear Teorías Físicas eligiendo la Teoría Matemática que proporciona a la descripción de los hechos mayor belleza. Pero ¿qué tipo de criterio es la belleza a la hora de elegir una teoría física?
Por una parte, la belleza de una teoría se remonta y se une a una tradición del pensamiento filosófico: la sencillez: se elige la teoría matemática que describe los hechos de la forma más sencilla (pensamiento de G. de Occam (1285-1347)) y con la la idea Leibniziana, que mantiene que, dada la infinita bondad de Dios, entre todas las posibilidades que se tenía para crear el mundo creó el mejor de los mundos, posibles porque y en un mundo así se debe dar la mayor cantidad deseable de cosas con el menor gasto que se pueda pensar y tenía que ser el más bello.




