
Las ecuaciones diferenciales constituyen la columna vertebral de la mecánica newtoniana. Las fuerzas atractivas entre dos cuerpos vienen dadas por la ley de Gravitación Universal, que es una ecuación diferencial no lineal.
La ley de Gravitación permitió deducir, entre otras cosas, la forma elíptica de las órbitas de los planetas alrededor del Sol. Recordemos que J. Kepler (1571-1630) dedujo, a partir de las observaciones de T. Brahe (1546-1601), que las trayectorias de los planetas alrededor del Sol eran elípticas y que, más tarde, I. Newton (1642-1727) explicó el movimiento de todos los cuerpos celestes con la ley de la Gravitación que decía un cuerpo atraía a los demás que lo rodean y que esa fuerza atractiva que existía entre dos de ellos era directamente proporcional al producto de sus masas e inversamente al cuadrado de la distancia que los separaba.
A partir de la Ley se explicaban los movimientos de los planetas alrededor del Sol y se hacían cálculos precisos que permitían determunar las localizacionis de los astros en el firmamento. Sin embargo, aunque las predicciones que aportaban los cálculos astronómicos realizados con las leyes matemáticas eran precisos y coincidían con las observaciones realizadas, aparecieron pequeñas discrepancias entre las observaciones y las predicciones, así como ciertas preguntas a las que no se conseguía responder adecuadamente.
Las discrepancias procedían del hecho de que las leyes funcionaban bien para un sistema a dos cuerpos, pero en el universo, interactuaban muchos objetos celestes que interactuaban entre si. Newton demostró la elipse perfecta de las órbitas de los planetas que predecía la Ley se cumplía casi a la perfección; pero también observó que la influencia atractiva de los demás planetas y satélites, que no mantenían siempre la misma posición relativa hacían que las órbitas sufrieran ciertas desviaciones y se pensó en la posibilidad de que los planetas pudieran salir de sus órbitas teóricas y llegaran a desestabilizar el Sistema Solar. Con esta observación se comenzó a estudiar cómo afectaría a la órbita de un astro que girara alrededor de otro la influencia gravitatoria de un tercero. Durante todo el siglo XVIII este problema conocido como el problema de tres cuerpos fue abordado por muchos matemáticos y de forma particular en los sistemas Sol-Tierra-Luna y Sol-Júpiter-Saturno.
El problema de los tres cuerpos, se puede formular de la siguiente forma: determinar en cualquier instante las posiciones y las velocidades, de tres cuerpos con masa que se encuentran sometidos a la atracción mutua dada por la Ley de Gravitación Universal, partiendo de posiciones y velocidades iniciales dadas. Este problema eraestaba claramente relacionado con la estabilidad del Sistema Solar. Podía ocurrir, bajo determinadas condiciones, que el sistema evolucionara alcanzando grandes velocidades que hicieran que los astros abandonaran sus órbitas y se desestabilizara el sistema.
P. S. Laplace (1749-1827) abordó el problema y estudió del movimiento de los cuerpos con más masa del sistema Solar y observó que Júpiter aceleraba su marcha a la vez que Saturno ralentizaba su movimiento. Si estos movimientos orbitales continuaban su evolución en ese sentido indefinidamente, Júpiter se estrellaría contra el Sol y Saturno acabaría saliendo del Sistema Solar. Pero Laplace demostró que las perturbaciones en las velocidades se debían al movimiento elíptico de los planetas y que su efecto no era acumulativo sino periódico. Y, si las perturbaciones eran periódicas y sus efectos acotados el proceso sería reversible. Laplace demostró que cada cuatrocientos cincuenta años el comportamiento de Júpiter y Saturno cambiaba, entonces: Júpiter deceleraba y Saturno se aceleraba y, de ese modo, las órbitas permanecerían estables sin una variación desestabilizante.
El problema de los tres cuerpos fascinó a los mejores matemáticos, J. L. Lagrange (1736-1813) demostró que si los tres cuerpos ocupaban los vértices de un triángulo equilátero y dos de ellos tenían masas muy grandes en relación con la del tercero, era posible dar con una solución exacta. Estos vértices se conocen en astronomía como puntos lagrangianos. En 1906 fueron descubiertos tres asteroides, en la posición de Lagrange llamados asteroides troyanos.

Un siglo más tarde, H. Poincaré (1854-1912), demostró la no-integrabilidad (no era resoluble por cuadraturas) de las ecuaciones de la dinámica celeste y las limitaciones de las técnicas tradicionales para el cálculo de las órbitas. Aunque las soluciones por los métodos del cálculo numérico proporcionaban buenas aproximaciones durante un tiempo finito, no permitían garantizar la estabilidad del Sistema Solar durante un tiempo indefinido. Sin embargo, era posible generar por métodos numéricos fragmentos de órbitas calculados mediante la integración numérica. Un procedimiento que no pudo desarrollar completamente Poincaré. Pero que los ordenadores realizan de manera eficaz.
Para el caso n = 3 resulta difícil o imposible encontrar fórmulas explícitas para ellas. Hasta la fecha, a pesar de los potentes ordenadores modernos y los siglos de trabajo de brillantes matemáticos y físicos, solo disponemos de fórmulas explícitas para cinco familias de órbitas, tres de ellas halladas por L. Euler (en 1767) y dos por J. L. Lagrange (en 1772).
Trabajos de complejidad matemática parecida a los expuestos, pero realizados con la ayuda de los ordenadores, permitieron el alumbramiento de la Teoría del Caos que surgió con la informática en la década de 1970. Los ordenadores permitieron la visualización de la evolución de sistemas dinámicos complejos, como el Sistema Solar. Y fue, precisamente el problema de tres cuerpos en interacción gravitatoria, como la del Sol, la Tierra y la Luna, un claro antecedente de la teoría del caos.
La teoría del caos pone de manifiesto que no podemos calcularlo todo, ni hacer previsiones a largo plazo, aunque dispongamos de ecuaciones deterministas.
El sistema siguiente sistema de ecuaciones diferenciales ordinarias, conocido como sistema Lorenz-Saltzman, es un sistema no lineal y determinista. Las ecuaciones que lo forman representan transferencia de calor por convección en la atmósfera, y, por tanto, es un modelo simple de dinámica de la atmósfera. En el sistema x, y, z son variables reales que dependen a su vez de la variable tiempo.
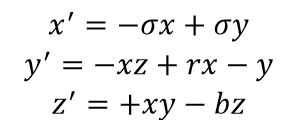 Siendo, σ: el número de Prandtl, r: número Rayleigh, b: razón entre la longitud y altura del sistema. La variable x representaba la velocidad y la dirección de circulación del aire (si x > 0 el aire circula en sentido horario mientras que si x < 0 lo hará en sentido contrario a las agujas del reloj. La variable y significaba la variación de temperatura vertical, y la variable z era la desviación del gradiente vertical de temperatura de la linealidad. Se toman los parámetros σ = 10, r = 28 y b = 8/3, donde el modelo de Lorenz exhibe un comportamiento caótico
Siendo, σ: el número de Prandtl, r: número Rayleigh, b: razón entre la longitud y altura del sistema. La variable x representaba la velocidad y la dirección de circulación del aire (si x > 0 el aire circula en sentido horario mientras que si x < 0 lo hará en sentido contrario a las agujas del reloj. La variable y significaba la variación de temperatura vertical, y la variable z era la desviación del gradiente vertical de temperatura de la linealidad. Se toman los parámetros σ = 10, r = 28 y b = 8/3, donde el modelo de Lorenz exhibe un comportamiento caótico

E. Lorenz (1917-2008) era un meteorólogo del MIT que, en 1960, estaba trabajando con el sistema de ecuaciones Lorenz-Saltzman para hacer predicciones del tiempo atmosférico. Como el sistema era no lineal (en la segunda ecuación está el producto xz y en la tercera xy) no era integrable y trataba de resolverla numéricamente con la ayuda de ordenadores, cuando, observó que algo raro ocurría cuando repetía cálculos con valores iniciales muy próximos. He aquí como él mismo reconstruyó los acontecimientos y su reacción en su libro, La esencia del caos (1993) (en Español: Ed Debate)
En un momento dado, decidí repetir algunos de los cálculos con el fin de examinar con mayor detalle lo que estaba ocurriendo. Detuve el ordenador, tecleé una línea de números que había salido por la impresora un rato antes y lo puse en marcha otra vez. Me fui al vestíbulo a tomarme una taza de café y regresé al cabo de una hora, tiempo durante el cual el ordenador había simulado unos dos meses de tiempo meteorológico. Los números que salían por la impresora no tenían nada que ver con los anteriores. Inmediatamente pensé que se había estropeado alguna válvula o que el ordenador tenía alguna otra avería, cosa nada infrecuente, pero antes de llamar a los técnicos decidí comprobar dónde se encontraba la dificultad, sabiendo que de esa forma podría acelerar la reparación. En lugar de una interrupción brusca, me encontré con que los nuevos valores repetían los anteriores en un principio, pero que enseguida empezaban a diferir, en una, en varias unidades, en la última cifra decimal, luego en la anterior y luego en la anterior. La verdad es que las diferencias se duplicaban en tamaño más o menos constantemente cada cuatro días, hasta que cualquier parecido con las cifras originales desaparecía en algún momento del segundo mes. Con eso me bastó para comprender lo que ocurría: los números que yo había tecleado no eran los números originales exactos sino los valores redondeados que había dado a la impresora en un principio. Los errores redondeados iniciales eran los culpables: se iban amplificando constantemente hasta dominar la solución. Dicho con terminología de hoy: se trataba del caos.
Un simple redondeo, una pequeña variación en las condiciones iniciales, de milésimas, que se va ampliando con e paso del tiempo. Algo tan pequeño y tan sutil como el batir de las alas de una mariposa se puede percibir como un vendaval al otro lado del mundo. La imagen de algo pequeño que se va amplificando continuamente está recogida en un proverbio chino con el nombre de efecto mariposa. Este concepto ha quedado vinculado a la Teoría del Caos; el aleteo de una mariposa en Hong Kong puede desatar una tormenta en Nueva York.
Víctor Arenzana Hernández

