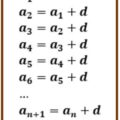
Los griegos estaban firmemente convencidos de que una magnitud cualquiera, M, se podía medir con una magnitud de la misma especie, u, que se tomaba como unidad, y que la medida de M se podía expresar en función de u y partes alícuotas suyas. Así, podríamos expresar que la medida de M es de 4 u, 3 décimas de u de u y cuatro centésimas.
Pero, hacia el siglo V antes de Cristo, los Pitagóricos descubrieron la existencia de las magnitudes inconmensurables, cuya medida no se podía expresar en términos de una unidad y sus partes alícuotas. El descubrimiento se produjo, seguramente, al intentar medir la diagonal del cuadrado tomando como unidad el lado y partes alícuotas del mismo. El hallazgo de este tipo de magnitudes despertó un recelo hacia los procesos infinitos que se acabó por expulsar de las matemáticas los procedimientos infinitos y a negar la existencia de infinito actual.
Y es que el hecho de que no pudiera medirse con partes alícuotas del lado unidad fue una sorpresa que rompía con la idea de que todo debía tener una medida exacta, de que cada medida debía ser un número y que, además ese número debía ser racional. Por otra parte, el descubrimiento cuestionaba la hipótesis de que la materia estuviera formada por átomos, al menos iguales, ya que no se concebía que la materia se pudiera dividir indefinidamente hasta desvanecerse en la nada sin llegar a encontrar una unidad indivisible de medida.
A partir de la introducción del sistema de numeración decimal posicional, las operaciones con números, pero, sobre todo, al resolver ecuaciones algebraicas con coeficientes racionales, aparecieron como raíces de las ecuaciones, además de los números enteros positivos y los racionales, los números negativos, expresiones radicales y números complejos. Es decir, el conjunto de los números racionales se amplió a otro conjunto numérico con un conjunto de números (los números algebraicos) algunos de los cuales que no se no se podían expresar en forma de fracción, eran irracionales, pero empezaban a tomar sentido como números.
Los números irracionales que se conocían eran los números algebraicos que habían surgido de la resolución de ecuaciones. Es cierto que habían aparecido otros números, como el número e o el número π, que no eran soluciones de las ecuaciones algebraicas, pero habían surgido en la Geometría o en el campo del Análisis y se consideraban como constantes numéricas, sin hacerse muchas preguntas sobre su procedencia.
El número π simplemente se consideraba como la relación entre la longitud de la circunferencia y su diámetro. De hecho el símbolo π procede del griego περιφέρεια (periferia) y fue utilizado por primera vez en 1706 por W. Jones (1675-1749) y difundido en la obra de L. Euler (1707-1783). Igualmente, el número e se convirtió en un número importante, porque fue la base de los logaritmos neperianos, se utiliza en economía para el cálculo de interés continuo, interviene en el tiempo de la desintegración radiactiva, el desarrollo en serie de ex, permitió relacionar a la función exponencial con las funciones trigonométricas, … pero, a pesar de ser un número tan importante, no aparece como solución de ninguna ecuación algebraica.
Los números que no son soluciones de ecuaciones algebraicas con coeficientes racionales se llaman trascendentes. Sabemos que hay muchos más números que trascendentes que algebraicos, sin embargo, no es fácil demostrar que un número es trascendente.
Se conocen relativamente pocos y algunos tienen nombre, algunos: 2√2, π, e, Ln2, Ω (constante de Chaitin), número de Louiville, …, indudablemente, muchos otros que permanecen en el anonimato. Y es que los números algebraicos se pueden generar con un procedimiento general: la resolución de ecuaciones algebraicas, mientras que los números trascendentes son descubiertos uno a uno y si queremos saber si un número es trascendente tenemos que demostrar que no hay ecuación algebraica que lo tenga por solución. Es más fácil demostrar que hay infinitos números trascendentes y que el conjunto tiene la potencia del continuo que determinar si un número es trascendente o no lo es.
De hecho, hasta 1873 no demostró Ch. Hermite (1822-1901) que el número e era trascendente. En realidad demostró que eα (α ≠ 0 ) eraun número trascendente. Está demostración fue generalizada por C.L.F. von Lindemann (1852-1939) y demostró, utilizando la fórmula de Euler eπi + 1 = 0, que π era un número trascendente. (ver https://www.gaussianos.com/como-demostrar-que-%CF%80-pi-es-trascendente/)
El teorema de Hermite Lindeman demuestra que si un número α ≠ 0 es algebraico (sobre Q), entonces eα es trascendente. En particular, e y π son trascendentes.
Después de los estudios de G. Cantor (1845-1918) y de R. Dedekind (1831-1916) sobre los conjuntos numéricos y la teoría de conjuntos se pudo demostrar que, cuando se completaban los números algebraicos para formar el conjunto de los números reales, este conjunto de números reales era infinitamente más grande que el de los algebraicos. Para hacernos una idea de la relación entre el cardinal del conjunto de los números algebraicos y el cardinal del conjunto de los números reales recurriremos al cálculo de probabilidades. ¿Cuál será la probabilidad de que eligiendo un número al azar en el intervalo real (0,1) obtengamos un número algebraico?
En primer lugar, el intervalo real (0,1), tiene infinitos números reales y también infinitos números algebraicos. Aplicando la definición de probabilidad de Laplace de cociente entre casos favorables y casos posibles, la probabilidad sería ∞/∞ es decir indeterminado.
Podemos no considerar al segmento real (0, 1) como un conjunto de infinitos puntos, sino como un conjunto de medida (longitud) 1 – 0 = 1. Podemos preguntarnos cuál será la longitud del conjunto de los números racionales denso en (0,1) (o de los números algebraicos). Con esta consideración pasaremos de considerar las probabilidades como cociente entre número de elementos al cociente entre longitudes
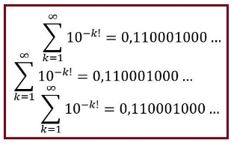
Como los números algebraicos son conjuntos numerables, se pueden representar en una sucesión: a1, a2, a3, …, an, … contenida en el intervalo real (0,1) y midamos su longitud. Para ello cubramos a1 con un intervalo simétrico, centrado en a1, de diámetro 1/10, cubramos a2 con un intervalo simétrico, centrado a2, en de diámetro 1/102, a3 con un intervalo de diámetro 1/103 y así sucesivamente.
Los puntos del conjunto de la sucesión están contenidos dentro del conjunto de intervalos que hemos definido, cuya suma de longitudes es:
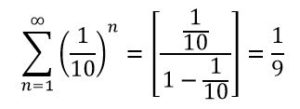
Pero el diámetro de los intervalos podría tener una longitud arbitraria y tan pequeña como queramos, que designaremos ε .
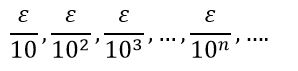
Entonces:
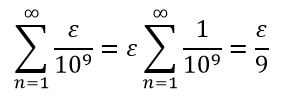
Como ε es arbitrario, la longitud puede ser tan pequeña como se quiera, por tanto, la sucesión de números algebraicos tiene medida (longitud).
Luego, si elegimos al azar un número del intervalo real (0,1), la probabilidad de que sea un número algebraico será: 0/1 = 0, lo que significa que hay muchísimos más números trascendentes que algebraicos.