
La ley de la reflexión de la luz era conocida desde la antigüedad. En un tratado de Catóptrica atribuido a Euclides (323-285 a.C.) se recogía en la proposición primera:
En los espejos planos, convexos y cóncavos los rayos visuales se reflejan formando ángulos iguales.
En la obra euclidiana explicaba mediante los principios de la óptica geométrica las imágenes formadas en los espejos mediante el principio de que el ángulo de incidencia era igual a ángulo de reflexión.
R. Descartes (1596-1650), en su Dióptrica de 1637, comparaba la reflexión de la luz con el rebote de una pelota sobre una superficie lisa y pulimentada. Mientras que el fenómeno de la refracción de la luz dependía de la consistencia, solidez y dureza de las partículas que formaban los cuerpos transparentes que atravesaba el rayo luminoso.
Pierre Fermat (1601-1665) planteó la propagación de la luz partiendo de un principio extremal, que requería el cálculo de máximos o mínimos. El Principio de Fermat afirmaba que: la trayectoria que recorre un rayo de luz entre dos puntos dados es aquella en la que emplea un tiempo mínimo. Y como la velocidad de la luz era constante, la trayectoria para el tiempo mínimo entre dos puntos debía ser la línea de mínima distancia, que en el espacio ordinario era la línea recta
El Principio de Fermat plantaba el comportamiento de determinados fenómenos físicos en términos de minimización de una función y sería el comienzo de muchas teorías físicas como el Principio de Mínima Acción, que dio lugar a las ecuaciones de Euler- Lagrange, que se derivaban de la minimización de un funcional cuyos extremos se mantenían fijos.
Del Principio de Fermat se puede deducir la ley de la reflexión (ángulo de incidencia igual al ángulo de reflexión) de la siguiente manera:
Se trata de probar que si la luz va de un punto A a otro B reflejándose en un espejo plano la trayectoria desde A al espejo sumada con la distancia del espejo a B es de longitud mínima. cuando el ángulo de incidencia es igual al ángulo de reflexión:
Si la luz va de A a B reflejándose en un espejo por el camino de mínima distancia. El rayo de luz debe tocar al espejo en un punto I’ tal que la suma de distancias AI’ + I’B sea mínima.
Consideremos el punto B’, simétrico de B respecto al espejo, como IB = IB’, es evidente que:
AI’ + I’B = AI’ + I’B’
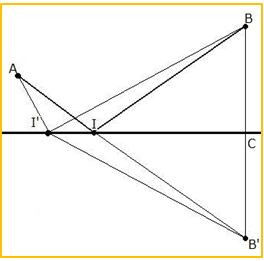
Por el Principio de Fermat, la luz recorrería el camino (virtual) de A a B’ por el camino de mínima distancia. Para que la suma de distancias AI’ + I’B’ sea mínima, es necesario que A, I’ y B’ estén alineados, es decir que I’ ocupe el lugar I de la figura, entonces. es evidente que:
ángulo BIC = ángulo CIB’ por simetría axial respecto al espejo y que
ángulo CIB’= ángulo CII’ por ser ángulos opuestos por el vértice.
Luego el ángulo de incidencia es igual al ángulo de reflexión.
Este resultado permite resolver algunos problemas relacionados con la simetría y el juego del billar como:
Problema 1.- En la orilla derecha de un río se encuentran un caballo A y su establo C. La distancia entre A y C es de 3 km. La distancia del caballo al río es de 2 km. y la distancia del establo el río de 3 km. Calcula la distancia mínima que tiene que recorrer el caballo para ir al establo después de haber abrevado en el río.

Solución: La mínima distancia para ir de A a C, parando por el río será, por las condiciones de mínimos explicadas para la reflexión, igual a la distancia AC’(siendo C’ el punto simétrico de C respecto al río), que podemos calcular fácilmente a partir del triángulo rectángulo sombreado.
El cateto AR lo podemos calcular como cateto del triángulo ACR, donde AC, mide 3km y RC mide 1km, por lo tanto:
![]()
Como RC’ mide 5 km, el camino de mínima distancia que tiene que recorrer el caballo será:
![]()
Problema 2.- ¿Cuál es el camino mínimo que tiene que recorrer una bola de billar A para ir a para a chocar con la bola B después de haber rebotado en dos bandas perpendiculares? Calcular la longitud de la trayectoria en el caso que la situación de las bolas sea A (2,5) y B (7,3)

Solución: La trayectoria de longitud mínima se deberá hacer eligiendo un punto Q en una banda de manera que
AQ + QP + PB sea mínimo.
Sea A’ el simétrico de A, respecto a la banda vertical y B’ el simétrico de B respecto a la banda horizontal, entonces
AQ + QP + PB sea mínimo A’Q + QP + PB’ mínimo,
lo que implica que los puntos A’QPB’ deben estar alineados, según indica la figura.
Si A (2,5) y B (7,3), es claro que, tomando la esquina como origen de coordenadas:
A’ (-2,5) y B (7,-3), y la distancia será:
![]()
Problema 3.- ¿Cuál es el camino mínimo que tiene que recorrer una bola de billar A para ir a para a chocar con la bola B después de haber rebotado en dos bandas paralelas? Calcular la longitud de la trayectoria en el caso que la situación de las bolas sea A(6,15) y B(20,4). La anchura de la mesa es 20.
Respuesta: La bola A puede tocar en primer lugar la banda superior o la inferior como se puede observar en las trayectorias (1) o (2) que se indican en las figura:
Tomando como origen de coordenadas la esquina inferior. En el caso (1). Si A (6,15) y B (20,4), es claro que A’ (6,25) y B’ (20, -4)
![]()

En el caso (2), tomando, igualmente, como origen de coordenadas la esquina inferior
Si A(6,15) y B(20,4), es claro que A’(6,-15) y B’(20, 32)
![]()
Por lo que la distancia mínima se da en el caso (1) y es 32,2




