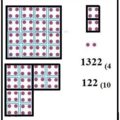
Nuestro sistema numérico actual apareció en la Europa occidental a través del mundo árabe. En su difusión tuvo una importancia capital el matemático árabe Muhammad ibn Musa abu Djafar Al-Khwarizmi (780-850). Gracias a sus escritos el sistema numérico indoarábigo se aceptó en el mundo árabe como algo, no solamente interesante en las contabilidades y en las transacciones comerciales, sino que también se adoptó como un recurso importante para el avance de las matemáticas.
El primer escrito occidental en el que aparecieron los números indoarábigos fue en el Codex Vigilanus, de autor anónimo, escrito en el año. El manuscrito fue copiado y ampliado en 976 por un monje llamado Vigila del Monasterio benedictino de San Martín de Albelda (La Rioja).
En realidad el Codex Vigilanus no era un tratado de matemáticas ni tampoco era el lugar más adecuado para albergar la numeración indoarábiga, pero Vigila la describió en un pequeño apéndice en el que explicaba, de forma breve, su superioridad tanto en la aritmética (que seguía el sistema aditivo de la numeración romana) como en el cálculo. Ahora bien, describir el sistema de numeración en un libro e introducir y difundirlo en una sociedad son dos cosas diferentes. ¿Cómo se extendió y se impuso la numeración indoarábiga (y los nuevos métodos de cálculo introducidos por ella) por Europa?
En esta historia tuvo un papel muy importante el monje benedictino francés Gerberto de Aurillac (946-1003) aficionado a las matemáticas que estudió en el monasterio de Santa María de Ripoll (Gerona). situado en la Marca Hispánica del Imperio Carolingio con Al-andalus. La Marca era una amplia zona fronteriza de la península en la que convivían hispanorromanos, iberos, celtas, judíos, árabes, bereberes y godos en la que había comercio y se utilizaba la nueva numeración. Allí aprendió Gerberto el nuevo sistema de numeración, desde allí lo introdujo en el Imperio Carolingio y más tarde propició su difusión en todo el mundo cristiano primero como monje y mucho más desde que fue nombrado Papa en 999 con el nombre de Silvestre II.
Pero la vía de aceptación más importante de los nuevos números fue la de los comerciantes y mercaderes. En los mercados, los intercambios de dinero eran rápidos y constantes y llevar una contabilidad ágil tenía un sentido práctico. En este campo el matemático italiano Leonardo de Pisa (1170-ca1250), también conocido como Fibonacci, dio un salto de gigante con su Liber Abaci (1202). Fibonacci fue educado en Bugía (Argelia), donde su padre era funcionario de aduanas y representaba a los comerciantes de la República de Pisa. Leonardo viajó mucho con su padre y reconoció las enormes ventajas de los sistemas de cálculo usados en los países que visitó. y fue en ese terreno práctico donde aprendió el ábaco, al uso de los indios, es decir, en la práctica comercial y en sus libros, aprendió entre árabes el sistema de numeración de los indios y también descubrió muchas de sus aplicaciones.
Fibonacci estructuró y presentó todos estos conocimientos en Liber Abaci, una obra que fue modelo de muchas aritméticas posteriores. En el libro, que llegó a ser ampliamente copiado e imitado se estudiaban el sistema de numeración posicional decimal indo-arábigo y las operaciones con los números árabes, también estudiaba ecuaciones de primer y segundo grado y sistemas de ecuaciones y recogía muchos de los problemas similares a los aparecidos en las fuentes árabes.
Cuando el emperador del Sacro Imperio Romano Germánico Federico II (1194-1250) quiso controlar el comercio y la industria para recaudar impuestos necesitó funcionarios civiles formados en aritmética, en contabilidad y en cálculo para lo que en 1224 fundó la Universidad de Nápoles en la que se estudiaba Liber Abaci.
En 1240 la ciudad de Pisa, le concedió a Fibonacci un sueldo vitalicio para reconocerle los servicios prestados a la ciudad de Pisa en enseñanza de cálculos para mercaderes y comerciantes y, en general, por su contribución a la instrucción de sus conciudadanos.
Costó más de quinientos años sustituir la numeración romana por la nueva numeración, pero la transformación fue tan amplia y fructífera para el comercio y para la ciencia que algunos autores la han calificado a este proceso de revolución comercial, en una evocación a la Revolución Industrial del siglo XIX.
PROBLEMA 1.- LOS ÁRBOLES DEL REY
Un rey envió 30 hombres a plantar árboles y plantaron 1000 árboles en 9 días. ¿Cuántos días tardarán 36 hombres en plantar 4400 árboles?
Solución: 33 días, ya que:
Un hombre plantará 1000/30 árboles en 9 días, por lo tanto:
Un hombre plantará 1000/270 árboles en 1 día, lo que significa que:
36 hombres 36000/270 árboles en 1 día, simplificando la fracción:
36 hombres 400/3 árboles en 1 día, como hay que plantar 4400 árboles, multiplicamos por 11, luego:
36 hombres 4400/3 árboles en 11 días y, por lo tanto:
36 hombres plantarán 4400 árboles en 33 días
PROBLEMA 2.- TREINTA PÁJAROS POR 30 DENARIOS
Un hombre compra 30 pájaros entre perdices, pichones y gorriones. Se gasta 30 denarios. Si una perdiz cuesta 3 denarios, un pichón 2 y dos gorriones cuestan un denario, ¿cuántos pájaros compró el hombre de cada tipo?
Solución: Sea x el número de perdices, y el número de pichones y z el número de gorriones, los datos nos permiten plantear el siguiente sistema de ecuaciones:
x + y + z = 30 3x + 2y + z/2 =30
Despejando x y z en función de y:
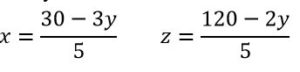
Como x e y deben ser enteros y positivos, por lo tanto, 30 – 3y debe ser múltiplo de 5 y la única solución posible es y = 5, que también hace que 120 – 2y sea múltiplo de 5.
x =3 y = 5 y z = 22
PROBLEMA 3.- DOS VIAJEROS
Dos hombres tienen la intención de hacer un largo viaje. Uno de ellos caminará 20 millas diarias. El otro hará una milla el primer día, 2 el segundo, 3 el tercero y así sucesivamente añadiendo siempre una milla a lo recorrido el día anterior. ¿Cuántos días tardará el segundo viajero en alcanzar al primero?
Solución: Supongamos que tarde x días en alcanzarlo. El primero recorrerá 20x millas y el segundo habrá recorrido 1 + 2 + 3 + ··· + x millas, es decir:
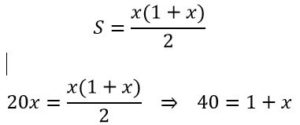
⇒ x =39, luego tardará 39 días
PROBLEMA 4.- OTROS DOS VIAJEROS.
Dos hombres tienen la intención de hacer un largo viaje. Uno de ellos caminará 10 millas diarias. El otro hará 3 millas el primer día, 6 el segundo, 9 el tercero y así sucesivamente, añadiendo siempre tres millas a lo recorrido el día anterior. ¿Cuántos días tardará el segundo viajero en alcanzar al primero?
Solución: Supongamos que tarde x días. El primero recorrerá 10x milla y el segundo habrá recorrido 3 + 6 + 9 + ··· + 3x millas, es decir:
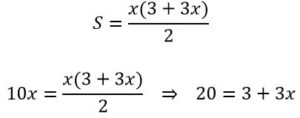
⇒ x =17/3, tardará 17/3 días
PROBLEMA 5- EL PANECILLO
Si 1/3 de un panecillo vale 1/4 de un besante, ¿cuánto cuesta 1/5 de panecillo?
Solución: Si 1/3 de un panecillo vale 1/4 de un besante, un panecillo costará 3/4 de besante. Luego un 1/5 de panecillo costará 3 /20 de besante
PROBLEMA 6.- DOS NÚMEROS ENTEROS
Encuentra dos números enteros de manera que los 2/7 de uno sean igual que los 3/8 del otro.
Solución: Sean los números enteros x e y. Se cumple que:
![]()
Como x e y deben ser enteros una solución trivial es x = 21 e y =16.
En realidad hay infinitas soluciones x = 21n e y =16n, con n = 1,2,3, …
PROBLEMA 7.- TRES NÚMEROS ENTEROS
Encuentra tres números enteros de manera que los 2/5 de uno sean igual que los 3/7 del segundo e igual que los 4/9 del tercero.
Solución : Sean los números x, y, z
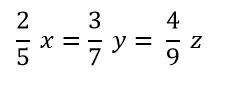
⇒ 2·7·9 x = 3·5·9y = 4·5·7 z ⇒
Expresando x y z en función de y:
![]()
Los valores que hacen enteros a x e y serían los múltiplos de 28, tomando y = 28, una solución será:
y = 28 x =30 z =27