
Los libros de aritmética tradicionales, hasta mediados del siglo pasado mantenían una clasificación de los problemas en diferentes tipos. Eran unas agrupaciones que reunían problemas que suponían diferentes aspectos concretos de la proporcionalidad, de proporcionalidad. Así, recogían problemas de interés comercial, de grifos, de mezclas, de aleaciones de móviles, etc. Hoy vamos a abordar un tipo de problemas que es un caso particular de este último, el problema de relojes. La decisión de encuadrar los problemas dentro de un marco conocido de la vida cotidiana facilita la comprensión de las cuestiones con las que puede experimentar (en este caso con tal de disponer de un reloj con esfera analógica de manecillas) y en el caso de los problemas de relojes nos sitúa ante cuestiones preliminares de observación astronómica. Ya que se trata, en esta materia se aborda muchas veces, cuestiones como la de calcular el tiempo que debe transcurrir, entre dos conjunciones de astros sucesivas, problema semejante al de calcular en tiempo que transcurre entre dos superposiciones sucesivas de las saetas del reloj.
Las disposiciones que suelen requerirse con una mayor frecuencia son: Que las manecillas estén superpuestas (conjunción), que estén situadas en ángulo recto (cuadratura) o que determinen un ángulo llano (oposición).
En particular en los problema de relojes regla general y es que el ángulo o arco que recorre el minutero (aguja mayor) en un tiempo dado es 12 veces mayor que el que describe la manecilla horaria.
Problema 1: Un reloj marca las 3 en punto. ¿A qué hora entre las 3 y las 4 se superpondrán las agujas?
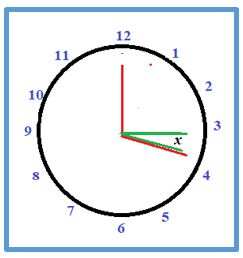
Solución: Sea x el arco (medido en minutos de hora) que describe la aguja intervalo, necesitamos que el minutero se encuentre entre los números 3 y 4, por lo que el arco del minutero debe ser 15 + x. Por la regla que fundamental tendremos que
15 + x =12x ⇒ 11x = 15 ⇒ x = 15 /11 = 1,36 min = 1min y 22seg.
Por lo tanto, las agujas se superpondrán un minuto y 21 segundos después de la tres y cuarto, es decir a las 3 h 16 min 22 seg
Problema 2: Un reloj marca las 3 en punto. ¿A qué hora entre las 4 y las 5 se superpondrán las agujas?
Solución: Sea x el arco (medido en minutos de hora) que describe la aguja horaria. Como se superpondrán las agujas entre las 4 y las 5, Como se las agujas se superponen en ese intervalo, necesitamos que el minutero se encuentre entre los números 3 y 4, por lo que el arco del minutero debe ser 20 + x. Por la regla fundamental tendremos:
20 + x =12x ⇒ 11x = 20 ⇒ x = 20 /11 = 1,89 min = 1min y 49seg.
Por lo tanto, las agujas se superpondrán un minuto y 49 segundos después de la cuatro y veinte y cuarto, es decir: 4 h 21 min 49 seg
Problema 3: Un reloj marca las 2 en punto. ¿A qué hora formarán sus agujas por primera vez un ángulo recto?
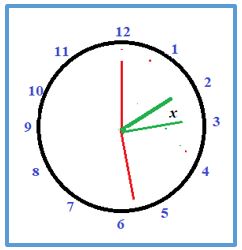
Solución: Puesto que queremos que las agujas formen un ángulo recto, debemos tener una diferencia de 15 minutos entre las agujas.
Ahora bien, la aguja horaria se encuentra en el 2, entonces para que la diferencia entre las agujas sea de 15 minutos el minutero debe estar pasado el 5 (ya que la aguja horaria también se moverá), es decir, las agujas del reloj forman un ángulo recto a las 2 h 25 min y un poco más, a ese poco más lo llamaremos x. Sea x el arco que describe la aguja horaria y sea 25 + x el arco que describe el minutero, entonces de la regla tendremos que:
10 + x + 15 = 12x ⇒ 35 =11x ⇒ x = 25 /11 = 2,27 = 2m 16 seg
Formarán ángulo recto por primera vez a: 2horas, 27min, 16seg
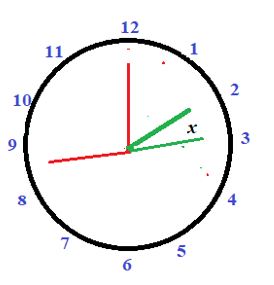
Problema 4: Un reloj marca las 2 en punto. ¿A qué hora formarán sus agujas por primera vez un ángulo de 180º?
Solución: Puesto que queremos que las agujas formen un ángulo llano, debemos tener una diferencia de 30 minutos de tiempo entre las agujas. Ahora bien, la aguja horaria se encuentra en el 2, entonces para que la diferencia entre las agujas sea de 30 minutos se debe tener que el minutero esté entre las 8 y las 9 (ya que la aguja horaria también se moverá), es decir, las agujas del reloj forman un ángulo llano a las 2 h 40 min y un poco más, a ese poco más lo llamaremos x. Sea x el arco que describe la aguja horaria, el arco que describe el minutero 10 + x + 30, entonces por la regla fundamental tendremos que:
10 + x + 30 = 12x ⇒ 40 = 11x ⇒ x = 40 /11 = 3,63 = 3min y 38 seg
Luego formarán las agujas un ángulo llano 2 horas, 43min, 38seg
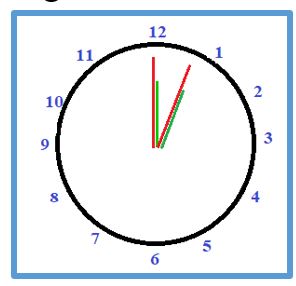
Problema 5.- Un reloj marca las 12 en punto ¿A qué hora volverán a estar las agujas superpuestas?
Solución: El horario recorre x, y el minutero 60 + x , luego, por la regla fundamental:
60 + x = 12x ⇒ 60 = 11 x ⇒ x = 5.45 ⇒ x = 5 min 27s
