
Una Progresión Aritmética es una sucesión numérica, en la cual, la diferencia entre dos términos consecutivos es un valor fijo, d, que se llama diferencia.
Es decir, es la sucesión a1, a2, a3, . . ., an, … donde an – an-1 = d. En estas progresiones el termino general se puede expresar en función del primer término y de la diferencia d según la expresión:
an = a1+ (n-1) d.
Se puede observar que el término general de una progresión aritmética es un polinomio de primer grado en n.
an = d n + (a1–d) = a n + b, donde a = d y a1– d = b
Existen progresiones aritméticas de orden superior y se pueden clasificar según el grado del polinomio en que se puede expresar el término general de la misma.
Definición: Una progresión aritmética de segundo orden es una sucesión numérica cuyo término general es un polinomio de segundo grado en n, es decir an = an2 + bn + c
Proposición: En una progresión aritmética de segundo orden cada término se obtiene del anterior sumando sucesivamente los términos de una progresión aritmética de primer orden,
Demostración: Basta ver que las diferencias entre dos términos consecutivos cualesquiera forman una progresión aritmética de primer orden, es decir, un polinomio de primer grado en n
an – an-1 = an2 + bn + c – [a(n-1)2 + b(n–1) + c] =
= an2 + bn + c – [an2 -2an + a + bn – b + c] =
= an2 + bn + c – an2 + 2an – a – bn + b – c = 2an + (b – a)
Que es un polinomio de primer grado en n.
Ejemplo: La sucesión de los cuadrados: {an}= {n2}= {1, 4, 9, 16, 25,…} es una progresión aritmética de segundo orden, ya que el término general es un polinomio de segundo grado. Y la sucesión de las diferencias entre dos términos consecutivos es la progresión aritmética de los números impares:
{an – an-1}= {n2 – (n-1)2} = {2n-1}= {1, 3, 5, 7, 9, 11, …}
Ejercicio 1: Calcula el término general de la progresión aritmética de orden superior:
1, 5, 14, 28, 47, 71, 100,…
Respuesta: En efecto es una progresión aritmética de orden superior, ya que la diferencia de términos consecutivos es la progresión aritmética:
4, 9, 14, 19, 24 29
Podemos escribir las diferencias en la forma:
1, 5, 14, 28 , 47, 71 , 100
4, 9, 14, 19, 24 29
5, 5, 5, 5 5
Con lo que el término generalde la prgresión aritmética de segundo orden será: an = P(n) = an2+ bn + c
Para calcular a, b y c usaremos el método de los coeficientes indeterminados

Luego a = 5/2, b =-(7/2), c =2 y, por lo tanto, an = (5/2)n2 – (7/2)n + 2
Ejercicio 2: Hallar el término general de la progresión de segundo orden:
{4, 9, 17, 28, 42, 59, 69, …}
Respuesta: En efecto es de segundo orden, ya que sus diferencias sucesivas forman una progresión aritmética de primer orden:
4 9 17 28 42 59 69 …
5 8 11 14 17 20 …
3 3 3 3 3…
El término general de la progresión aritmética de segundo orden será un polinomio de segundo grado:
an = P(n) = an2+ bn + c, cuyos coeficientes a, b y c calcularemos por el método de los coeficientes indeterminados:
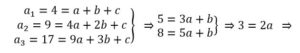
Ejercicio 3.– Término general de la progresión aritmética de orden superior:
{4, 6, 10, 16, 24, 34… }
Respuesta: Es de segundo orden, por lo tanto: an = P(n) = an2+ bn + c
4, 6, 10, 16, 24, 34 …
2, 4, 6, 8 10…
2, 2, 2, 2 …
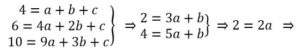
Luego a = 1, b = -1, c =4 y, por lo tanto, an = n2 – n + 4
Ejercicio 4 – Calcula la suma de los n primeros términos de la progresión aritmética de segundo orden:
{k(k-1)} k=1…n
Respuesta: Recordaremos la fórmula de la suma de los cuadrados de los n primeros números naturales:

Debemos calcular:

Ejercicio 5.- Calcula la suma de los 100 primeros términos de la progresión aritmética de segundo orden {k(k-1)} k = 1,…,n
Respuesta: Por resultado del ejercicio anterior:
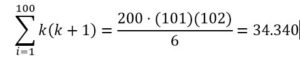
Ejercicio 6.- Calcula la suma de los 100 primeros términos de los inversos de la progresión aritmética de segundo orden {i(i-1)} i = 1….
Respuesta: Descomponiendo en fracciones simples:
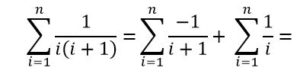
= – (1/2 ) – (1/3) – …. – (1/101) + 1+ (1/2 ) + (1/3) – …. + (1/100) = 1– (1/101) = 100/101




