El teorema de Pitágoras y sus propiedades han despertado la curiosidad de los matemáticos desde los comienzos de los estudios de la geometría. La relación fundamental entre tres segmentos rectilíneos de longitudes a, b, c que cumplían la relación a2 + b2 = c2 y que, además, los segmentos de longitudes a y b fueran perpendiculares fascinó a muchas mentes y desde en el antiguo Egipto se le encontraron multitud de aplicaciones. El triángulo rectángulo de lados 3, 4, y 5 fue la escuadra de los agrimensores egipcios.
Evidentemente, los triángulos rectángulos más fáciles de manejar son aquellos cuyas longitudes de sus lados son número naturales. Euclides en sus Elementos encontró unas fórmula para hallar las medidas de los lados de los triángulos rectángulos con lados de medida entera. El trío numérico que forma la medida de estos lados se llama terna pitagórica. En este trabajo vamos a hacer una aproximación a las propiedades elementales, que tienen las ternas pitagóricas exponiendo en primes lugar unas definiciones para disponer de una terminología común.
Definición.- En un triángulo rectángulo, los lados menores, a y b, que son los que forman el ángulo recto, se llaman catetos y el lado mayor, c, se llama hipotenusa.
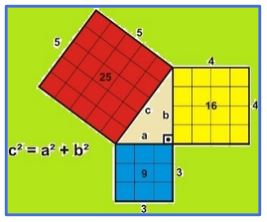
Teorema de Pitágoras: El área del cuadrado cuyo lado es la hipotenusa es igual a la suma de las áreas de los cuadrados cuyos lados son los catetos.
Expresado en forma aritmética a2 + b2 = c2
Terna pitagórica: Llamaremos terna pitagórica a un trio de números naturales ordenados de menor a mayor (a, b, c) que cumple el teorema de Pitágoras a2 + b2 = c2. Y el triángulo formado por los lados a, b, c se llama triángulo pitagórico.
Terna pitagórica primitiva. – La terna pitagórica (a, b, c) es pitagórica es primitiva si los tres números que la integran son primos entre si o, equivalentemente, si mcd (a, b, c) = 1, o no tienen ningún divisor común).
Observación: En una trío cualquiera de números enteros (que no sea pitagórica) mcd (x, y, z) = 1, no significa que cada pareja de números sean primos entre si, por ejemplo: mcd (6, 11, 15) = 1 y, mcd (6, 15) = 3. Pero en el caso de las ternas pitagóricas mcd (a, b, c) = 1 es equivalente a que mcd (a, b) = mcd (a, c) = mcd ( b, c) = 1
Propiedad 1. – La terna a, b, c es pitagórica es primitiva si y solo si a, b, y c son primos dos a dos
Dem: Si d = mcd (a, b) > 1 ⇒ d divide a a y d divide a b. y como a2 + b2 = c2 ⇒ d divide a c. Y divide al mcd (a, b, c) = 1,
Si Supongamos que mcd (a, b, c) = d ⇒ d divide a a y a b por tanto al mcd (a, b) = 1 , por tanto d =1
Propiedad 2. – Si la terna (a, b, c) es pitagórica y k es un entero positivo cualquiera la terna (ka, kb, kc) también lo es.
Dem: Si la terna a, b, c es pitagórica:
a2 + b2 = c2 ⇒ k2 (a2 + b2) = k2c2 ⇒ k2a2 + k2b2 = k2c2 ⇒ (ka)2 + (kb)2 = (kc)2, luego la terna (ka, kb, kc) es pitagórica.
FIBONACCI Y LA SUMA Y DIFERENCIA DE CUADRADOS:
Propiedad 3.– La suma de los impares consecutivos es un cuadrado, es decir, 1 + 3 + 5+ ···+ (2n-1) = n2
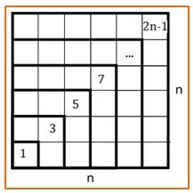
S = 1 + 3 + ··· + (2n-3) + (2n-1)
S = (2n-1) + (2n-3) + ···· + 3 + 1
Sumando ambas igualdades:
2S = 2n + 2n + + 2n + 2n
2S = n·2n ⇒ S= n2.
Fibonacci: aprovechó esta propiedad de forma ingeniosa
Propiedad 4: Todo cuadrado impar se puede expresar como diferencia de dos cuadrados
Demostración :
Si a2 es impar ⇒ a2 = 2n -1 ⇒ ocupa el lugar n = (a2 + 1)/2. El impar anterior a a2 será a2 – 2 de la ocupa n = (a2 – 1)/2.
1 + 3 + 5 + ···+ (a2 -2 ) = M = m2es un cuadrado y
[1 + 3 + 5 + ···+ (a2 -2 )] + a2 = M’ = m’2 también es cuadrado.
Evidentemente m’2– m2= a2
Ejemplo : Expresa el número 63 como diferencia de dos cuadrados
63 = 2n-1 ⇒ n= 31 (teniendo en cuenta que 2n -1 = n2 – (n – 1)2) 63 = 322 -312.
Propiedad 5.– Propiedades de paridad de las ternas primitivas (a, b, c)
- a, b y c no pueden ser todas pares
- a, b y c no pueden ser todas impares
- No puede haber dos pares.
- Tiene que haber dos impares y una par.
- c es impar.
- a, b uno es par y otro impar
Si (a, b, c) es una terna pitagórica primitiva entonces los números a, b, c son primos relativos dos a dos, así que no hay dos de ellos pares. (La ternas pitagóricas fundamentales cumplen que mcd (a, b) = mcd (a, c) = mcd ( b, c) = 1). Por otro lado, como a, b, c satisfacen a2 + b2 = c2 no pueden ser todos impares, ya que a2 + b2 sería par y c2 es impar, En consecuencia uno y sólo uno de los números a, b, c es par.
De esta reflexión se puede deducir el siguiente resultado.
Propiedad 6.- Si (a, b, c) es una terna pitagórica primitiva entonces exactamente uno de a, b es impar y la hipotenusa c es impar.
Resumiendo: Una propiedad que cumple, las ternas pitagóricas fundamentales es que al menos uno de los números a o b es par y c siempre es impar.
Propiedad 7.- Si (a, b, c) es una terna pitagórica fundamental, c no es múltiplo de tres
Demostración: a ≡ 0,1,2 (mod 3) igualmente b ≡ 0,1,2 (mod 3) ⇒ a2 ≡ 0, 1 (mod 3) e b2 ≡ 0,1 (mod 3), como a e b son primos entre sí, no pueden tener divisores comunes, lo que significa que no pueden darse el caso de que a2 ≡ 0 (mod 3) e b2 ≡ 0 (mod 3) a la vez, ya que la terna pitagórica no sería fundamental y, como a2 + b2 = c2, c no es múltiplo de tres.
Propiedad 8: Si Si (a, b, c) es una terna pitagórica fundamental, entonces , a o b es múltiplo de tres (sólo uno de los dos)
Demostración:
- Si 3 dividiera a a entonces, como mcd (a, b) = 1, Luego el 3, que es divisor de a, no divide a b.
- Si 3 no divide a a entonces a2 ≡ 1 (mod 3) y como, por la propiedad anterior, c no es múltiplo de tres c2 ≡ 1 (mod 3), peo entonces c2 – a2= b2 ≡ 0 (mod 3). Luego el 3, que no divide a a, divide a b