
El Cañón de Newton es un modelo utilizado comúnmente para ilustrar la generación de una órbita alrededor de la Tierra. La representación consiste en un cañón situado en la cima de una montaña disparando sus proyectiles horizontalmente. La montaña debe ser muy alta para evitar el rozamiento de la bala del cañón con la atmósfera terrestre. Para pequeñas velocidades de lanzamiento, el proyectil cae sobre la superficie terrestre, pero, cuando la velocidad aumenta progresivamente, llega un momento en el cuerpo lanzado ya no cae, llega a chocar con el propio cañón y, finalmente, a velocidades muy muy grandes, la bala escapa del campo gravitatorio terrestre. I. Newton (1643-1727) lo expresa así:
De los movimientos de los proyectiles se comprende que los planetas pueden ser retenidos en órbitas ciertas mediante fuerzas centrípetas. Una piedra lanzada, sometida a la a la acción de su gravedad, se desvía de la trayectoria rectilínea y describiendo una curva en el aire y cae al suelo; si se lanzase con mayor velocidad, llegaría más lejos. Aumentando la velocidad podría lograrse que describiera un arco de una milla, dos, cinco, diez …y, por fin, más allá de los límites de la Tierra, que no cayese al suelo.
Sea AFC la superficie de la Tierra, sea C su centro y sean VD, VE, VF las líneas descritas por el proyectil desde el vértice V de un monte muy alto, líneas paralelas a la línea del horizonte, resultado de lanzamientos sucesivos. (Suponemos que el aire no ofrece resistencia alguna) Si se aumenta la velocidad la piedra llegará aún más lejos, hasta F y hasta G; finalmente, si se aumenta la velocidad continuamente sobrepasará el monte desde el que fue lanzada. Como el área descrita por el radio que unía a la piedra con centro de la Tierra [Prop I del Libro I de Principia Mathematica] será proporcional al tiempo, su velocidad al regresar al monte no será menor que al principio y, manteniendo la velocidad puede así girar muchas veces por la misma ley.
Newton acaba afirmando que, si los cuerpos son lanzados desde la cima del monte según líneas horizontales desde alturas de cinco, diez, cien millas e incluso de varios semidiámetros terrestres; según las distintas velocidades y según las distintas fuerzas de gravedad existentes en cada región, los cuerpos describirán arcos terrestres, concéntricos o de excentricidades diferentes. Y los cuerpos lanzados recorrerán los cielos con esas trayectorias de forma semejante a los planetas.
VELOCIDAD DEL SATÉLITE QUE DESCRIBE UNA ÓRBITA CIRCULAR
Supongamos un cuerpo de masa m (satélite) que se mueve con un movimiento circular de radio r alrededor de un cuerpo mucho mayor que él de masa M. La fuerza de atracción gravitatoria entre ellos será:

Por otra parte, la aceleración centrípeta de m, siendo r el radio de la órbita circular que describe m, alrededor de M será: a = v2/r. Aplicando la Segunda Ley de Newton, F = m ·a, resulta:

Es decir, que si elevamos un cuerpo a una distancia r (medida desde el centro de la Tierra) y le imprimimos una velocidad v se mantendrá en órbita.
VELOCIDAD DE ESCAPE
Se llama velocidad de escape de un objeto lanzado en el campo gravitatorio de un planeta a la velocidad mínima de lanzamiento que permite escapar del campo gravitatorio y llegar fuera de él con velocidad cero. Expresado de forma matemática es la mínima velocidad de lanzamiento que le permite llegar al infinito con velocidad nula.
El objeto tiene que ser lanzado con la suficiente velocidad para que pueda abandonar completamente la atracción gravitatoria del planeta (que supondremos que es la Tierra de masa MT y radio RT), situación que se dará cuando la distancia entre el planeta y el objeto sea infinita. En ese momento, el objeto estará en reposo y su energía mecánica se anulará (Ya que tanto la energía cinética como la potencial serán cero).
Para calcular la velocidad de escape utilizaremos el principio de conservación de la energía mecánica entre la superficie terrestre y el infinito:
- La energía mecánica es la suma de la energía cinética y la energía potencial gravitatoria, que expresaremos así: Em = Ec + Ep.
- La energía mecánica se conserva, por lo tanto, será la misma en la superficie de la Tierra que en el infinito, es decir:
![]()
- La energía cinética de un cuerpo de masa m es Ec = m·v2/2
- La energía potencial gravitatoria de un cuerpo de masa m a una distancia r del centro de la Tierra es Ep = – G·MT ·m /r (MT es la masa de la Tierra)
Inciso: Recordemos que Energía Potencial Gravitatoria es el trabajo que se debe realizar para trasladar una masa m desde el infinito hasta la posición inicial Si el campo gravitatorio es el terrestre y el cuerpo de masa m está sobre la superficie terrestre (a una distancia RT del centro:

Aplicando el principio de conservación de la energía entre la superficie y el infinito:
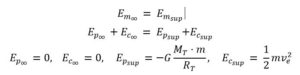
Por lo tanto, la velocidad de escape, ve, será:
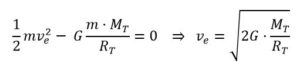
Se observa que la velocidad de escape es independiente de la masa del cuerpo (satélite) lanzado y sólo depende de la masa del planeta y del radio del mismo (realmente, de la distancia respecto de su centro a la que se produce el lanzamiento).
La velocidad de escape de la Tierra puede calcularse sabiendo que la constante de gravitación universal G = 6,67·10-11 N·m2/kg2, la masa de la Tierra, MT = 5.972·1024 kg y el radio de la Tierra RT = 6,371·106 m

En el siglo XVIII adelantaron la idea de agujero negro; el astrónomo inglés John Michel (1724-1793) y P.S. Laplace (1749-1827) se plantearon el problema de determinar que radio debía tener una estrella como el Sol de forma que ni su propia luz pudiera escapar de su campo gravitatorio (es decir, que radio debía tener para convertirse en Agujero Negro). Para ello, la velocidad de escape ve debía ser igual a c, Esto es debía cumplir:
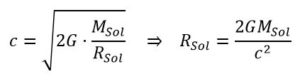
obtuvieron que el radio del Sol, para ser un agujero negro, debería ser de RSol = 2,9 km




