Pitágoras descubrió una conexión entre las matemáticas y la música que permitía relacionar las notas musicales con los números racionales. Para realizar sus investigaciones musicales inventó el monocordio, que era un instrumento de una sola cuerda con una caja de resonancia, un canon o regla graduada y un puente variable, que permitía hacer sonar diferentes longitudes de cuerda. Con el monocordio podía medir las relaciones numéricas entre diferentes longitudes de cuerda que emitían sonidos consonantes.
Los conceptos de consonancia y disonancia han variado a lo largo de la historia. Pero los sonidos son consonantes dependiendo del intervalo que los separa (intervalo musical es la relación entre las longitudes de las cuerdas que los emiten). Pitágoras constató que los sonidos eran consonantes cuando las longitudes de las cuerdas que los emitían se podían expresar como cociente de dos números enteros pequeños: 1, 2, 3, 4, 5, 6… Si la relación entre las longitudes fuera un “número raro” (129/47 o 97/43) los más seguro sería que los sonidos emitidos oídos conjuntamente resultaran disonantes.
Evidentemente el trasfondo físico es bastante más complejo, pero los pitagóricos llegaron a ver que: dos sonidos eran consonantes si la razón entre sus las longitudes era sencilla, por ejemplo 2/1 (octava), 3/2 (Quinta), 4/3(cuarta), 5/4 (tercera)… etc.
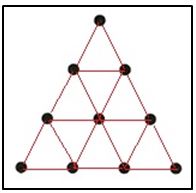
Tan grande les pareció este descubrimiento que a los números 1, 2, 3, 4 les llamaron la Tetraktys y su representación geométrica era la figura sagrada de los pitagóricos dentro de su numerología. En ella estaba encerrado el número perfecto 10 = 1 + 2 + 3 + 4 y en esos los cuatro primero números enteros estaba encerrada la armonía musical. Por ella los pitagóricos realizaban el juramento de hermandad, que lo hacían en nombre de Pitágoras, pero sin nombrarlo con la fórmula siguiente: por quién transmitió a nuestra alma la tetraktys.
La observación de Pitágoras se corresponde con la física de la cuerda vibrante que fue estudiada el siglo XVIII, momento histórico en el que las matemáticas estuvieron preparadas para abordar este problema físico. En 1715, B. Taylor (1685-1731) descubrió que el movimiento de un punto de la cuerda vibrante oscilaba como un péndulo simple y que, como consecuencia, la forma de la curva que tomaba la cuerda en un instante dado debería ser sinusoidal. En primer lugar se descubrió algo que conocía Pitágoras la relación entre la longitud de una cuerda que vibraba y la frecuencia de la nota emitida (aunque el filósofo griego no usara este concepto).
Sabemos que, cuando pulsamos una cuerda de guitarra la onda que llega a un extremo se refleja e interfiere con las ondas que llegan. Si las ondas producidas en esas reflexiones múltiples no coinciden en fase, la amplitud resultante será pequeña. Sólo para algunas frecuencias sucede que las ondas múltiplemente reflejadas estarán en fase resultando una onda estacionaria de gran amplitud. Éstas serán las frecuencias de resonancia del sistema y son justamente las frecuencias de los modos de vibración.
Las ondas que emiten esas frecuencias de resonancia deben ser aquellas cuya semilongitud de longitud de onda λ «quepa» en la cuerda vibtante de longitud L un número entero de veces. Es lo que ocurre el caso de una onda sinusoidal, en la que las longitudes de onda posibles serán aquellas cuya λ cumpla que : L = n (λ/2). Lo que conduce a que las λ posibles serán λ =(2L)/n, para n =1, 2, 3, 4…, números sencillos, tal y como como Pitágoras había descubierto de oído.
La cuerda de longitud L emite un sonido fundamental de una frecuencia f0. El problema físico parte de la velocidad de onda que propaga en una cuerda tensa que es
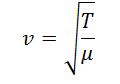
Donde T es la tensión de la cuerda y μ la densidad lineal de la misma. Por otra parte, sabemos que la velocidad de una onda es v = λ·f, es decir, que la frecuencia será f = λ/v.
De este modo, la cuerda de longitud L emite un sonido fundamental frecuencia f0, pero ese sonido no es el único que emite la cuerda al vibrar. También emite simultáneamente otros sonidos de menor intensidad. La distribución e intensidad de estos sonidos constitute el timbre que diferencia a los instrumentos o a las voces que cantan la misma nota.
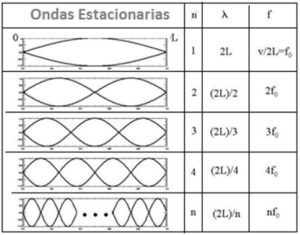
En el caso de los instrumentos de cuerda y viento, las frecuencias de estos sonidos acompañamtes son múltiplos de la frecuencia fundamental f0. De estos múltiplos (armónicos), el primero es la propia frecuencia fundamental, el segundo el doble 2 f0 el tercer armónico el triple 3 f0, etc.
Pitágoras no tenía afinador para conocer exactamente la frecuencia en Herzios de un sonido, ni siquiera un diapasón, pero él fue el primero en descubrir la relación entre los sonidos graves y los agudos y también que eran resultado de las características del cuerpo que los producía (tamaño, masa, tensión).
La frecuencia de la nota emitida y la longitud de la parte de cuerda del monocordio que vibraba eran inversamente proporcionales, y tenán la siguiente la relación:
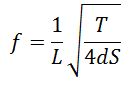LA AFINACIÓN
Pitágoras descubrió que al duplicar la frecuencia de una nota cualquiera (reducir a la mitad la longitud de la cuerda que vibraba), obtenía la misma nota más aguda o de mayor frecuencia. También descubrió que si una cuerda de longitud L emitía una nota de una determinada frecuencia, una cuerda de longitud 2L emitía la misma nota una octava más baja y una cuerda de longitud 4L emitía la misma nota dos octavas más bajas y una de longitud 2nL emite la misma nota n octavas más baja quela nota de partida.
Para hacer música hay elegir una escala, es decir, seleccionar un conjunto de notas (de frecuencias) que se utilizarán para elaborar melodías. Se puede plantear la cuestión de porqué se seleccionan unas notas determinadas y porqué no tocar con todas las frecuencias audibles dentro de ciertos límites. Un violín, un chelo o una viola podrían emitir todas la frecuencias dentro de un intervalo, pero otros instrumentos, por su diseño, como el piano o la flauta y la dulzaina sólo pueden emitir unas frecuencias determinadas.
Una vez aceptado como punto de partida que hay que elegir unas notas, que una frecuencia y su doble suenan bien tocadas simultáneamente y que, además, nuestro oído las reconoce como la misma nota, el problema se reducía a elegir qué otras frecuencias intermedias utilizar. Para ello, supongamos que nuestra nota más grave tiene frecuencia 1 (que llamaremos Do) y, por lo tanto, la de su doble tiene frecuencia 2 (será Do una octava más aguda). Nuestro problema se reduce entonces a decidir cómo elegimos las frecuencias intermedias consonantes con la nota fundamental Do dentro de una octava. Elegiremos notas consonantes con Do de frecuencia f , con el siguiente criterio:
Si 1 < f < 2 la aceptamos porque, ya es frecuencia intermedia entre 1 y 2.
Si f > 2 dividiremos f entre 2, 4, 8… ´hasta que la frecuencia de una octava suya, f’, esté entre 1 y 2
Si f < 2 multiplicaremos f por 2, 4, 8… ´hasta que la frecuencia de una octava suya esté entre 1 y 2
La elección de esta f se vio facilitada porque los griegos consideraban que la armonía consonante estaba en la santa Tetraktys, con los números enteros 1, 2, 3 y 4 y con ellos las frecuencias entre 1 y 2 serían 4/3 y 3/2 . Como dos notas cuyas frecuencias están en relación 3/2 (Intervalo de quinta) suenan bien al oído, la idea primera fue afinar por quintas, es decir, la de seguir añadiendo quintas y quintas de “quintas” entre 1 y 2 de cada una de las notas.
Con una quinta la escala tendría tres notas y quedaría: 1 < 3/2 < 2
Si añadimos la quinta de la quinta la frecuencia 3/2 x 3/2 = 9/4, pero como el resultado es mayor que 2, dividimos la frecuencia obtenida entre 2 y obtenemos la misma nota una octava más grave), obteniendo así la frecuencia 9/8.
La escala tendría cuatro notas y quedaría: 1 < 3/2 < 9/8 < 2
Siguiendo el procedimiento , es decir, en cada paso multiplicando la frecuencia de la última nota añadida por 3/2 y si el resultado es menor que 2 se añade a la escala la nota correspondiente y si no se le agrega la nota dividida entre 2.
Si llegáramos a la misma nota con la que empezamos o a una de frecuencia obtenida previamente, la escala estaría completa y pararíamos, ya que seguir no haría más que repetir las notas ya añadidas a la escala. Pero no sucederá así, ya que el algoritmo empleado consiste en multiplicar por 3/2 y, a veces, dividir por 2. Por lo que las frecuencias de todas las notas que se agreguen a la escala serán de la forma 3m/2n con m y n números enteros positivos y, como 2 y 3 son número primos entre si, la fracción es irreducible, por lo que nunca repetiremos frecuencia. Por lo tanto, hay que decidir cuando parar de añadir frecuencias y qué consonancias elegir.
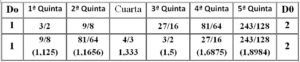
La primera afinación por quintas fue
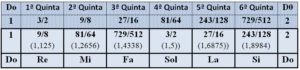
(en la fila tercera de la tabla aparecen las frecuencias ordenadas)
La tercera en esta escala (Mi) debería tener frecuencia 5/4 = 1,25, pero le corresponde 81/64 = 1,265625 y que resulta un poco disonante y se le suele llamar ditono pitagórico. Además, podrían haber mantenido la 6ª quinta 729/512 = 1,424, pero a los pitagóricos les pareció que servía mejor la cuarta 4/3 = 1,333, porque dividía la escala en siete intervalos cinco de mayor tamaño y dos claramente más pequeños. Los intervalos más pequeños se encuentran entre el Mi y el Fa, y entre el Si y el Do agudo.
El intervalo de Tono es 9/8 = 1,125 y el de semitono, aunque se denomina así no es la mitad, (media geométrica). El intervalo entre Mi y Fa es 1,0535, entre Si y Do 1,0535, que no coincide con
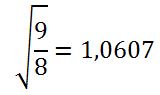
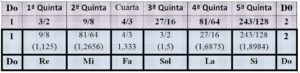
Los tonos y semitonos se pueden apreciar en el siguiente diagrama cartesiano Nota- Frecuencia
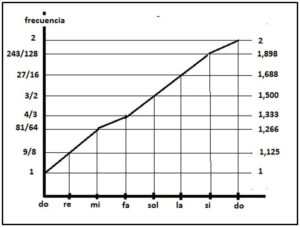
Donde se puede apreciar que existen siete intervalos cinco mayores (1,125) y dos que son la mitad:
Do 1,125 Re 1,125 Mi 1,053 Fa 1,125 Sol 1,125 La 1,125 Si 1,053 Do
La diferencia de frecuencias va aumentando según nos acercamos al agudo. No obstante, nosotros percibimos los intervalos de tono como iguales debido a que nuestra percepción de las frecuencias musicales es logarítmica lo que significa que nuestro oído percibe como intervalos iguales,
[f1, f2] y [2n·f1, 2n·f2]
Ya que
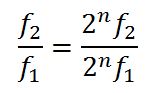
La afinación pitagórica fue efectiva mientras los intervalos armónicos de uso común fueron la octava, quinta y cuarta. Pero al final del siglo XII apareció la música polifónica en la que se acompañaba la voz de una melodía principal con otras voces diferentes, de forma que varias melodías se combinaban entre si según reglas y esquemas armónicos. Una de las voces seguía una tercera de la melodía fundamental para hacer duos y la polifinía se complicó aún con más en el Renacimiento con lo que la tercera pitagórica mostraba cada vez su disoncia y se hizo necesario buscar nuevos sistemas de afinación.
Auditivamente percibimos la distancia entre notas como algo lineal (la distancia de Do a Re es de un tono o una 2ª Mayor), pero físicamente se corresponde con el cociente entre las frecuencias de los dos sonidos.
