La paradoja de San Petersburgo fue formulada por primera vez por N. Bernoulli (1687-1759) en 1713, fue reformulada por su sobrino D. Bernoulli (1700-1782) y se publicaron en torno a ella muchas Memorias científicas en las Transacciones de la Academia de San Petersburgo. El problema que se plantea en la paradoja ponía de manifiesto el cuidado que había que tener con el manejo del infinito y que en, muchas situaciones, lo que se podía deducir para números grandes no se podía extender al infinito. La paradoja se puede formular así:
Pedro y Pablo juegan a cara o cruz. Lanzan al aire una moneda y si sale cara la primera vez Pedro paga 2€ a Pablo y el juego se acaba, si sale sólo cara la segunda tirada Pedro paga 4 €, si sale la tercera (y cruz en las anteriores) Pedro paga 8 €, si sale la cuarta por primera vez Pedro paga 16 € y así sucesivamente ¿Cuál debe ser la apuesta de Pablo para que el juego sea justo?
Para responder la pregunta debemos saber a qué se llama un juego de azar justo o equitativo: Dada una variable aleatoria discreta X aleatoria que toma los valores x1, x2, x3, …, xn con probabilidades p1, p2, p3, …, pn respectivamente se llama esperanza matemática o valor esperado de X a la suma de los productos de cada valor de la variable por la probabilidad con la que producen cada uno de los valores de la misma. Es decir:
E(X) = x1·p1 + x2· p2 + x3· p3 … + xn· pn
El nombre de valor esperado procede de los juegos de azar. Un juego que cumple que E(X) = 0, se llama juego equitativo, si E(X) > 0 es ventajoso para el jugador y si E(X) < 0 es desfavorable.
Está claro que Pablo:
Tiene la probabilidad 1/ 2 de ganar 2 € en la primera tirada, luego tiene la esperanza de ganar (1/2)·2 = 1€ en la primera tirada.
Tiene la probabilidad 1/ 4 de ganar 4 € en la segunda tirada, luego la esperanza de ganar (1/4)·22 = 1€ en la segunda tirada.
Tiene la probabilidad 1/ 8 de ganar 8 € en la tercera tirada, luego la esperanza de ganar (1/8)·23 = 1€ en la tercera tirada.
Y así sucesivamente, teniendo en cuenta el número de partidas la esperanza de Pablo será infinita.
Así que para jugar en este juego se necesitaría apostar una cantidad infinita.
Realmente pocos jugadores ocuparían el lugar de Pablo. Aunque sólo expusiera 50 € por participar en ese juego.
Si Pedro posee 100.000.000€, podría arriesgarse a jugar un número n de partidas tal que
2n ≤ 1000.000.000 ≤ 2n+1
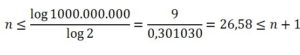
Es decir 26 partidas.
Resulta evidente que con 26 partidas la esperanza sería de 26 € y podría resultar adecuado apostar por ganar mil millones confiando en que salgan cruces en 25 lanzamientos y cara en el lanzamiento 26. A fin de cuentas apostamos con más riesgo en la Lotería de Navidad cuando jugamos décimo de 20 € Euros con la esperanza de ganar 300.000 € (antes de impuestos).