Georges L. Leclerc, Conde de Buffon (1707-1788), fue un naturalista francés que tuvo enorme influencia en las Ciencias Naturales de los siglos XVIII y XIX. Desde su puesto de administrador de los Reales Jardines Botánicos escribió una obra enciclopédica, que fue, seguramente, la primera versión naturalista de la historia de la Tierra. En su libro trató de explicar los fenómenos naturales aportando, única y exclusivamente, datos experimentales y explicaciones racionales, dejando de lado creencias tradicionales y presunciones religiosas.
En su obra Histoire naturelle, générale et particulière (1749-1788) reunió todo el saber de su tiempo en Biología, Geología, Historia Natural y Antropología y “solamente” pudo publicar treinta y seis volúmenes de cincuenta que tenía proyectados.
Buffon era un buen matemático y un experto en cálculo de probabilidades y, además, estaba interesado en descubrir las regularidades estadísticas de los procesos aleatorios en la línea marcada por Jakob Bernoullil (1654-1705) en su obra póstuma Ars Conjectandi (1713), Se planteó la siguiente cuestión de cálculo de probabilidades en la que aparecía el número π:
Sobre una superficie horizontal sobre la que están trazadas unas líneas paralelas equidistantes se lanza al azar una aguja perfectamente cilíndrica. Se pide calcular la probabilidad de que la aguja corte a una de las rectas paralelas.
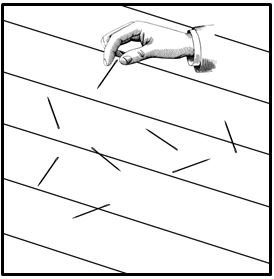
La solución del problema nos aporta una relación curiosa y es que si la longitud de la aguja es la mitad de la distancia entre paralelas la probabilidad es el inverso de π.
Y, en general, si llamamos 2a a la distancia entre las paralelas y L a la longitud de la aguja:
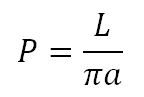
Si L = a, es decir, si la longitud de la aguja es la mitad de la distancia entre paralelas la probabilidad es 1/ π.
Resolveremos el problema con una aguja de 2cm lanzada al azar sobre un suelo en el que están dibujadas rectas paralelas separadas 4cm. Calcularemos la probabilidad de que, al lanzar la aguja sobre el suelo, corte a una de las rectas paralelas.
En primer lugar comenzaremos por dar un criterio para definir la posición de la aguja sobre el suelo respecto a las rectas paralelas para lo que elegiremos un extremo de la aguja como origen.
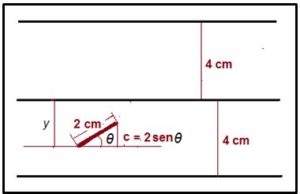
Si consideramos el esquema como un mapa elegiremos como origen el extremo de la aguja que queda más al sur y si la aguja queda paralela a las rectas paralelas del suelo elegimos el extremo de la aguja situado más al este.
Llamaremos y a la distancia de ese punto a la paralela más cercana a él situada al norte y designaremos con θ al ángulo formado por la aguja con una línea paralela las rectas paralelas del suelo que pasa por el extremo de la aguja.
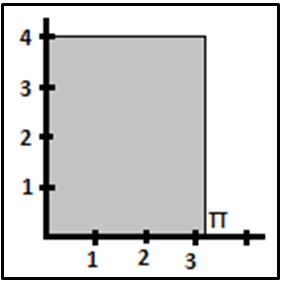
Es evidente que con los dos valores: (θ, y), que están acotados del modo siguiente: 0 ≤ y < 4, 0 ≤ θ < π, se pueden expresar todas las posibilidades que tiene la aguja al caer al suelo. Y se pueden representar en un rectángulo de área 4 π. Los puntos del rectángulo representan todas las formas posibles en las que puede caer la aguja sobre el suelo, es, por tanto, el conjunto de los casos posibles.
Ahora trataremos de distinguir, entre todos los posibles representados por el rectángulo, los casos favorables que serán aquellos en que la aguja corte a una de las paralela. Estos casos favorables se producirán cuando y < 2 Sen θ y 0 ≤ θ < π,
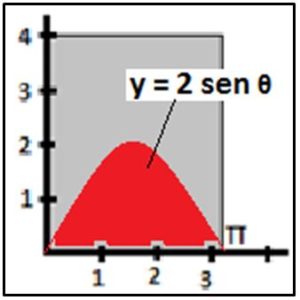
Representando gráficamente el conjunto de los puntos (θ, y) del rectángulo, serán los puntos de la superficie comprendida bajo la curva y = 2 Sen θ (representada en rojo)
Por lo tanto, la probabilidad de que la aguja corte a una de las paralelas trazadas en el suelo será:
Que es lo que habíamos afirmado al principio. Un siglo después J. E. Barbier (1839-1889) publicó en el Journal de mathématiques pures et appliquées, un artículo titulado Nota sobre el problema de la aguja y el juego de la articulación (1860). Que lo formuló así:
Si una línea poligonal cualquiera, cerrada o no, se lanza al azar sobre una hoja de papel en la que están trazadas unas líneas paralelas ¿Cuál será la esperanza matemática de que un jugador reciba un franco por cada punto de intercesión?
En esta situación, sin entrar en detalles, podemos hacer las siguientes consideraciones
a) La esperanza matemática de que la poligonal corte a una de las rectas paralelas del suelo será la suma de las esperanzas de cada uno de sus lados.
b) Esa esperanza matemática será proporcional a suma, L, de las longitudes de los lados de la poligonal.
c) Por tanto, la esperanza matemática será k·L, donde L es la longitud de la poligonal y k un factor de proporcionalidad que depende de cada poligonal. .
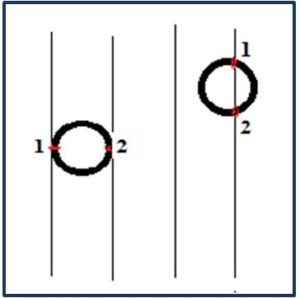
d) El resultado puede extenderse fácilmente a una poligonal regular de un gran número de lados, es decir, cuando la línea poligonal se transforma en curva (como ocurre con una sucesión de polígonos regulares de n lados cuando n → ∞, que tiende a una la circunferencia) Calculemos el valor k cuando la curva es una circunferencia de radio a a la que la lanzamos sobre un suelo en el que están trazadas unas rectas paralelas cuya distancia entre dos rectas consecutivas es 2a.
f) La esperanza matemática de que una circunferencia de radio a corte a las rectas paralelas equidistantes a una distancia 2a es 2. Ya que cada circunferencia o bien corta a una de las rectas paralelas en dos puntos o es tangente a dos líneas paralelas consecutivas, como se ve en la figura. Por tanto la esperanza matemática de este juego, es dos, ya que en cada lanzamiento recibirá de manera invariable 2€, por lo tanto:
k·L = 2 π a ·k = 2
Por lo tanto:
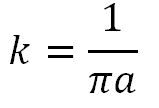
En particular, la esperanza matemática de una aguja de longitud L:
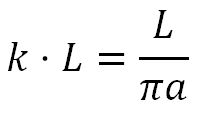
En el caso particular en el que la longitud L de la aguja sea menor que la separación entre dos paralelas consecutivas, la esperanza matemática es la misma que la probabilidad para que tenga intersección.
